Условие задачи:

Плотность воды 1000 кг/м³, а плотность камня 2500 кг/м³. Если не учитывать сопротивление воды при движении тела, то какую работу следует совершить при медленном подъеме камня массы 100 г в воде на высоту 80 см?

Задача №3.3.54 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_{в}=1000\) кг/м³, \(\rho=2500\) кг/м³, \(m=100\) г, \(h=80\) см, \(A-?\)

Решение задачи:

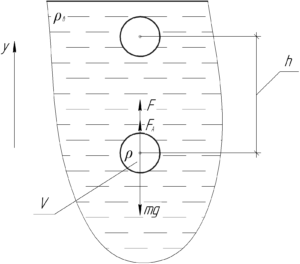Чтобы поднять камень, к нему нужно приложить некоторую силу \(F\). Если поднимать камень равномерно, то величину этой силы можно определить из первого закона Ньютона, записанного в проекции на ось \(y\):

\[F + {F_А} — mg = 0\]

\[F = mg — {F_А}\]

Работу \(A\) можно найти как произведение модуля силы \(F\) на модуль перемещения \(h\):

\[A = Fh\]

\[A = \left( {mg — {F_А}} \right)h\;\;\;\;(1)\]

Известно, что выталкивающую силу \(F_{А}\) и массу \(m\) можно определять по таким формулам:

\[{F_А} = {\rho _в}gV\]

\[m = \rho V\]

Тогда формула (1) для определения работы примет вид:

\[A = \left( {\rho Vg — {\rho _в}gV} \right)h = \left( {\rho  — {\rho _в}} \right)gVh\]

Неизвестный объем камня \(m\) выразим через известную массу камня \(m\) и его плотность \(\rho\):

\[V = \frac{m}{\rho }\]

В итоге мы получим такую окончательную формулу:

\[A = \left( {\rho  — {\rho _в}} \right)g\frac{m}{\rho }h\]

\[A = \left( {1 — \frac{{{\rho _в}}}{\rho }} \right)mgh\]

Переведем массу камня и высоту в систему СИ, а уже потом вычислим ответ:

\[100\;г = 0,1\;кг\]

\[80\;см = 0,8\;м\]

\[A = \left( {1 — \frac{{1000}}{{2500}}} \right) \cdot 0,1 \cdot 10 \cdot 0,8 = 0,48\;Дж\]

Ответ: 0,48 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.53 Плотность воды 1000 кг/м3, а плотность пробки 200 кг/м3. Пробковый шар массы 100 г
3.3.55 Палочка массы 400 г наполовину погружена в воду, как показано на рисунке. Угол
3.3.56 Палочка массы m наполовину погружена в воду, как показано на рисунке. Угол наклона