Условие задачи:

Плотность жидкости в 3 раза больше плотности материала тела. Какая часть объема тела будет выступать над поверхностью, если тело поместить в жидкость?

Задача №3.3.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_{ж}=3 \rho\), \(\frac{V_{н}}{V}-?\)

Решение задачи:

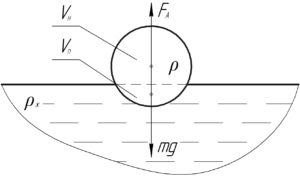Так как плотность тела \(\rho\) меньше, чем плотность жидкости \(\rho_{ж}\), то тело будет плавать, выступая над поверхностью воды. Запишем условие плавания тел:

\[{F_А} = mg\]

Тогда, подставив в это равенство выражения для определения силы Архимеда и массы, получим:

\[{\rho _ж}g{V_п} = \rho Vg\]

\[\frac{{{V_п}}}{V} = \frac{\rho }{{{\rho _ж}}}\]

Так как в условии сказано, что \(\rho_{ж}=3 \rho\), значит:

\[\frac{{{V_п}}}{V} = \frac{\rho }{{3\rho }} = \frac{1}{3}\]

Понятно, что полный объем тела \(V\) равен сумме объемов частей тела, которые находятся над и под водой.

\[V = {V_н} + {V_п}\]

Делим и левую, и правую часть этого равенства на \(V\):

\[\frac{{{V_н}}}{V} + \frac{{{V_п}}}{V} = 1\]

\[\frac{{{V_н}}}{V} = 1 — \frac{{{V_п}}}{V}\]

\[\frac{{{V_н}}}{V} = 1 — \frac{1}{3} = \frac{2}{3}\]

Ответ: 2/3.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.25 Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку
3.3.27 Полый цинковый шар, внешний объем которого 200 см3, плавает так, что половина его
3.3.28 Стеклянный шарик объемом 0,5 см3 равномерно тонет в воде. Какое количество