Условие задачи:

Поверх жидкости плотностью 1000 кг/м³ налита большим слоем жидкость плотностью 700 кг/м³, причем жидкости не смешиваются. Определить, какая часть объема тела плотностью 900 кг/м³ будет погружена в более плотную жидкость.

Задача №3.3.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\rho_1=1000\) кг/м³, \(\rho_2=700\) кг/м³, \(\rho=900\) кг/м³, \(\frac{V_1}{V}-?\)

Решение задачи:

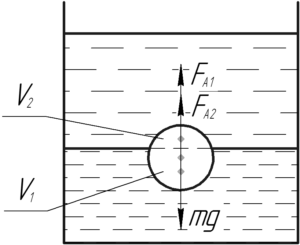На тело действуют две силы Архимеда (\(F_{А1}\) и \(F_{А2}\)) и сила тяжести \(mg\). Рассматриваемое тело будет плавать на границе раздела жидкостей. Запишем условие плавания тел:

\[{F_{А1}} + {F_{А2}} = mg\]

Распишем по формуле силы Архимеда в левой части, а в правой массу \(m\) представим как произведение плотности \(\rho\) тела на полный объем \(V\):

\[{\rho _1}g{V_1} + {\rho _2}g{V_2} = \rho Vg\]

\[{\rho _1}{V_1} + {\rho _2}{V_2} = \rho V\]

Поделим обе части равенства на \(V\):

\[{\rho _1}\frac{{{V_1}}}{V} + {\rho _2}\frac{{{V_2}}}{V} = \rho \;\;\;\;(1)\]

Понятно, что сумма частей объемов тела \(V_1\) и \(V_2\), находящихся в разных жидкостях, равна полному объему тела \(V\).

\[{V_1} + {V_2} = V\]

Также делим обе части полученного равенства на \(V\):

\[\frac{{{V_1}}}{V} + \frac{{{V_2}}}{V} = 1\]

\[\frac{{{V_2}}}{V} = 1 — \frac{{{V_1}}}{V}\]

Подставим это выражение в (1), тогда:

\[{\rho _1}\frac{{{V_1}}}{V} + {\rho _2}\left( {1 — \frac{{{V_1}}}{V}} \right) = \rho \]

\[{\rho _1}\frac{{{V_1}}}{V} + {\rho _2} — {\rho _2}\frac{{{V_1}}}{V} = \rho \]

Откуда искомая величина \(\frac{V_1}{V}\) равна:

\[\frac{{{V_1}}}{V} = \frac{{\rho  — {\rho _2}}}{{{\rho _1} — {\rho _2}}}\]

Произведем вычисления:

\[\frac{{{V_1}}}{V} = \frac{{900 — 700}}{{1000 — 700}} = 0,67\]

Ответ: 0,67.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.34 На рычажных весах уравновешен сосуд с водой. На сколько нужно увеличить массу гирь
3.3.36 Полый железный шар взвешивают в воздухе и керосине. Показания динамометра
3.3.37 Пустая цилиндрическая пробирка, опущенная вертикально в воду, оказалась погруженной