Условие задачи:
Предмет расположен перпендикулярно оптической оси собирающей линзы. На сколько процентов увеличится линейный размер его действительного изображения, если расстояние от предмета до переднего фокуса линзы уменьшить на 20%?
Задача №10.5.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a_2 =0,8a_1\), \(\alpha-?\)
Решение задачи:
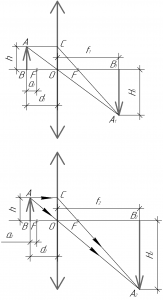 В условии задачи прямо написано, что мы имеем дело с собирающей линзой. Поскольку в обоих случаях собирающая линза дает действительное изображение, то для обоих случаев расстояние от линзы до предмета больше фокусного расстояния, т.е. предмет находится левее переднего фокуса линзы.
В условии задачи прямо написано, что мы имеем дело с собирающей линзой. Поскольку в обоих случаях собирающая линза дает действительное изображение, то для обоих случаев расстояние от линзы до предмета больше фокусного расстояния, т.е. предмет находится левее переднего фокуса линзы.
Искомое число процентов \(\alpha\) будем искать по следующей очевидной формуле:
\[\alpha = \frac{{{H_2} — {H_1}}}{{{H_1}}} \cdot 100\% \]
\[\alpha = \left( {\frac{{{H_2}}}{{{H_1}}} — 1} \right) \cdot 100\% \;\;\;\;(1)\]
Из подобия треугольников AOB и A1OB1 (верхний рисунок), AOB и A2OB2 (нижний рисунок) имеем следующие соотношения:
\[\left\{ \begin{gathered}
\frac{{{H_1}}}{h} = \frac{{{f_1}}}{{{d_1}}} \hfill \\
\frac{{{H_2}}}{h} = \frac{{{f_2}}}{{{d_2}}} \hfill \\
\end{gathered} \right.\]
Тогда, разделив нижнее уравнение на верхнее, получим:
\[\frac{{{H_2}}}{{{H_1}}} = \frac{{{f_2}{d_1}}}{{{f_1}{d_2}}}\;\;\;\;(2)\]
Запишем формулу тонкой линзы для собирающей линзы в общем виде:
\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\]
В этой формуле \(F\) — фокусное расстояние линзы, знак перед ним «+», поскольку линза — собирающая, \(d\) — расстояние от линзы до предмета, знак перед ним «+», поскольку предмет — действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) — расстояние от линзы до изображения, знак перед ним «+», поскольку изображение — действительное (то есть образуется на сходящемся пучке лучей — смотрите рисунок).
Выразим из формулы тонкой линзы расстояние \(f\):
\[\frac{1}{f} = \frac{1}{F} — \frac{1}{d}\]
\[\frac{1}{f} = \frac{{d — F}}{{dF}}\]
\[f = \frac{{dF}}{{d — F}}\]
Если принять, что расстояние от предмета до переднего фокуса равно \(a\), то имеем (то есть \(d — F = a\)):
\[f = \frac{{dF}}{a}\]
То есть:
\[\frac{f}{d} = \frac{F}{a}\]
В таком случае формула (2) примет вид:
\[\frac{{{H_2}}}{{{H_1}}} = \frac{{F{a_1}}}{{F{a_2}}}\]
\[\frac{{{H_2}}}{{{H_1}}} = \frac{{{a_1}}}{{{a_2}}}\]
Формула (1) станет такой:
\[\alpha = \left( {\frac{{{a_1}}}{{{a_2}}} — 1} \right) \cdot 100\% \]
По условию задачи расстояние от предмета до переднего фокуса линзы уменьшилось на 20%, то есть \(a_2 =0,8a_1\), поэтому:
\[\alpha = \left( {\frac{{{a_1}}}{{0,8{a_1}}} — 1} \right) \cdot 100\% \]
\[\alpha = \left( {\frac{1}{{0,8}} — 1} \right) \cdot 100\% = 25\% \]
Ответ: на 25%.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.56 От предмета высотой 20 см при помощи линзы получили действительное изображение
10.5.58 Точечный источник света находится на расстоянии 40 см от собирающей линзы
10.5.59 На каком расстоянии от рассеивающей линзы с фокусным расстоянием 10 см находится

 icodepro.ru
icodepro.ru