Условие задачи:
При торможении автомобиль, двигаясь равнозамедленно, проходит за пятую секунду 5 см и останавливается. Какой путь пройдет он за третью секунду этого движения?
Задача №1.3.52 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_5=5\) см, \(S_3-?\)
Решение задачи:
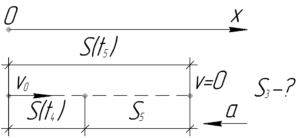 Распишем путь за пятую секунду как разность пути за \(t_5=5\) секунд и пути за \(t_4=4\) секунды.
Распишем путь за пятую секунду как разность пути за \(t_5=5\) секунд и пути за \(t_4=4\) секунды.
\[{S_5} = S\left( {{t_5}} \right) — S\left( {{t_4}} \right)\]
Движение автомобиля было равнозамедленным с некоторой начальной скоростью, поэтому:
\[{S_5} = {\upsilon _0}{t_5} — \frac{{at_5^2}}{2} — \left( {{\upsilon _0}{t_4} — \frac{{at_4^2}}{2}} \right)\]
\[{S_5} = {\upsilon _0}\left( {{t_5} — {t_4}} \right) — \frac{{a\left( {t_5^2 — t_4^2} \right)}}{2}\]
Из условия понятно, что всего тело двигалось \(t_5=5\) секунд, поэтому:
\[{\upsilon _0} = a{t_5}\]
Подставим это выражение в формулу пути за пятую секунду и выразим ускорение \(a\).
\[{S_5} = a{t_5}\left( {{t_5} — {t_4}} \right) — \frac{{a\left( {t_5^2 — t_4^2} \right)}}{2}\]
\[{S_5} = a\left( {t_5^2 — {t_5}{t_4} — \frac{{t_5^2}}{2} + \frac{{t_4^2}}{2}} \right)\]
\[{S_5} = \frac{a}{2}\left( {t_5^2 — 2{t_5}{t_4} + t_4^2} \right)\]
\[{S_5} = \frac{a}{2}{\left( {{t_5} — {t_4}} \right)^2}\]
\[a = \frac{{2{S_5}}}{{{{\left( {{t_5} — {t_4}} \right)}^2}}}\;\;\;\;(1)\]
Аналогично пути за пятую секунду \(S_5\) распишем искомый путь за третью секунду \(S_3\).
\[{S_3} = {\upsilon _0}\left( {{t_3} — {t_2}} \right) — \frac{{a\left( {t_3^2 — t_2^2} \right)}}{2}\]
\[{S_3} = a{t_5}\left( {{t_3} — {t_2}} \right) — \frac{{a\left( {t_3^2 — t_2^2} \right)}}{2}\]
\[{S_3} = \frac{a}{2}\left( {2{t_5}{t_3} — 2{t_5}{t_2} — \left( {t_3^2 — t_2^2} \right)} \right)\]
В конечном счеты мы получим следующую формулу для расчета ответа (подставив выражение (1) в последнюю формулу):
\[{S_3} = \frac{{{S_5}}}{{{{\left( {{t_5} — {t_4}} \right)}^2}}}\left( {2{t_5}{t_3} — 2{t_5}{t_2} — \left( {t_3^2 — t_2^2} \right)} \right)\]
Подставим числа, при этом переведем значение \(S_5\) из см в м.
\[{S_3} = \frac{{0,05}}{{{{\left( {5 — 4} \right)}^2}}}\left( {2 \cdot 5 \cdot 3 — 2 \cdot 5 \cdot 2 — \left( {{3^2} — {2^2}} \right)} \right) = 0,25\; м = 25\; см\]
Ответ: 25 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.51 Поезд метрополитена разгоняется от остановки с постоянным ускорением
1.3.53 Поезд, двигаясь от остановки с постоянным ускорением, прошел 180 м за 15 с
1.3.54 Точка движется вдоль оси x со скоростью, проекция которой v_x как функция

 icodepro.ru
icodepro.ru
Задача устная, если представить всё в виде графика.
Пока я показал только аналитическое решение, в будущем добавлю и графическое)
Здесь не сразу понял как в итоговой формуле для S3 1-ый множитель получился, после 5-ти минутного просмотра всех формул дошло, что там подставлена формула ускорения, делённая на 2, 2-ки сократились. В трудных задачах не всегда сразу видно какая формула из какой получается.
Советую не смотреть,а писать, повторяя действия) В этом случае вы ещё и запоминаете ход решения.
Иногда забываю объяснять подобные подстановки, хотя в Вашем случае очевидно, что в формулу подставили выражение для ускорения.