Условие задачи:
Пробежав с постоянным ускорением по взлетной полосе 750 м, самолет перед отрывом от земли имел скорость 270 км/ч. Какое время продолжался его разбег?
Задача №1.3.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=750\) м, \(\upsilon=270\) км/ч, \(t-?\)
Решение задачи:
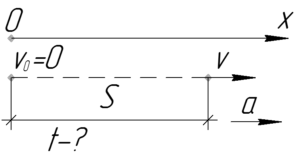 Формула скорости для равноускоренного движения имеет вид:
Формула скорости для равноускоренного движения имеет вид:
\[\upsilon = {\upsilon _0} + at\]
Также запишем формулу кинематики без времени:
\[{\upsilon ^2} — \upsilon _0^2 = 2aS\]
Учитывая, что самолет начинал движение без начальной скорости, то \(\upsilon_0=0\). Формулы примут следующий вид, запишем их в системе:
\[\left\{ \begin{gathered}
\upsilon = at \;\;\;\;(1)\hfill \\
{\upsilon ^2} = 2aS \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Из выражения (1) выразим искомое время разбега.
\[t = \frac{\upsilon }{a}\]
Из выражения (2) найдем ускорение \(a\) и подставим его в формулу выше.
\[a = \frac{{{\upsilon ^2}}}{{2S}}\]
\[t = \frac{{\upsilon \cdot 2S}}{{{\upsilon ^2}}} = \frac{{2S}}{\upsilon }\]
Переведем численное значение конечной скорости в систему СИ.
\[270\; км/ч = \frac{{270 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{2700}}{{36}}\; м/с = 75\; м/с\]
В итоге:
\[t = \frac{{2 \cdot 750}}{{75}} = 20\; с\]
Ответ: 20 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.49 Пуля, летящая со скоростью 141 м/с, попадает в доску и проникает на глубину
1.3.51 Поезд метрополитена разгоняется от остановки с постоянным ускорением
1.3.52 При торможении автомобиль, двигаясь равнозамедленно, проходит за пятую

 icodepro.ru
icodepro.ru
А нельзя было найти формулой нахождение времени?
Если Вы её здесь напишите, то я смогу ответить на Ваш вопрос
Есть формула s=(v+v0)t/2 ей можно на егэ пользоваться, не выводя её,?
Думаю, что можно