Условие задачи:
Протон и дейтрон (ядро изотопа водорода \(_1^2{\text{H}}\)), имеющие одинаковые скорости, влетают в однородное магнитное поле перпендикулярно линиям индукции. Как связаны между собой радиусы \(R_1\) и \(R_2\) окружностей, по которым, соответственно, движутся протон и дейтрон (массы протона и нейтрона считать равными)?
Задача №8.2.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=90^\circ\), \(\frac{R_2}{R_1}-?\)
Решение задачи:
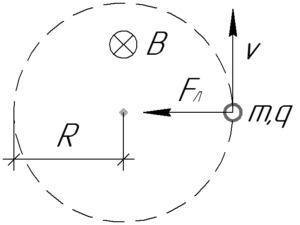 Для начала определимся с массами и зарядами. Протон имеет массу \(m_p\) и модуль заряда \(e\). Дейтрон (ядро атома изотопа водорода) \(_1^2{\text{H}}\) состоит из одного протона и одного нейтрона. Поэтому, если считать массы нейтрона и протона считать равными, его масса равна \(2m_p\), а модуль заряда равен \(e\).
Для начала определимся с массами и зарядами. Протон имеет массу \(m_p\) и модуль заряда \(e\). Дейтрон (ядро атома изотопа водорода) \(_1^2{\text{H}}\) состоит из одного протона и одного нейтрона. Поэтому, если считать массы нейтрона и протона считать равными, его масса равна \(2m_p\), а модуль заряда равен \(e\).
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
\[{F_Л} = B\upsilon q\sin \alpha \;\;\;\;(1)\]
Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость частицы, \(q\) — модуль заряда частицы, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. Мы в этой задаче имеем дело с положительно заряженными частицами, тогда в нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца будет направлена влево.
Сила Лоренца \(F_Л\) сообщает частице центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:
\[{F_Л} = m{a_ц}\;\;\;\;(2)\]
Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]
Подставим (3) в (2), тогда:
\[{F_Л} = \frac{{m{\upsilon ^2}}}{R}\;\;\;\;(4)\]
Приравняем правые части (1) и (4):
\[B\upsilon q\sin \alpha = \frac{{m{\upsilon ^2}}}{R}\]
Имеем:
\[Bq\sin \alpha = \frac{{m\upsilon }}{R}\]
Откуда радиус траектории \(R\) равен:
\[R = \frac{{m\upsilon }}{{Bq\sin \alpha }}\]
Запишем формулу для определения радиуса окружностей, по которым движутся протон и дейтрон (касаемо их зарядов и масс читайте первый абзац решения):
\[\left\{ \begin{gathered}
{R_1} = \frac{{{m_p}\upsilon }}{{Be\sin \alpha }} \hfill \\
{R_2} = \frac{{2{m_p}\upsilon }}{{Be\sin \alpha }} \hfill \\
\end{gathered} \right.\]
Разделим нижнее равенство на верхнее, тогда:
\[\frac{{{R_2}}}{{{R_1}}} = 2\]
Ответ: \(\frac{R_2}{R_1}=2\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.25 Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают
8.2.27 Протон и дейтрон (ядро изотопа водорода 2H1) влетают в однородное магнитное поле
8.2.28 Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции

 icodepro.ru
icodepro.ru