Условие задачи:
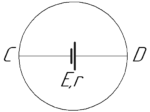 Проволока из нихрома изогнута в виде кольца радиусом 1 м. В центре кольца помещен источник тока с ЭДС 2 В и внутренним сопротивлением 1,5 Ом. Элемент соединен с точками C и D кольца по диаметру с помощью такой же нихромовой проволоки сечением 1 мм2. Определить разность потенциалов между точками C и D.
Проволока из нихрома изогнута в виде кольца радиусом 1 м. В центре кольца помещен источник тока с ЭДС 2 В и внутренним сопротивлением 1,5 Ом. Элемент соединен с точками C и D кольца по диаметру с помощью такой же нихромовой проволоки сечением 1 мм2. Определить разность потенциалов между точками C и D.
Задача №7.2.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(r_{рад}=1\) м, \(\rm E=2\) В, \(r=1,5\) Ом, \(S=1\) мм2, \(U-?\)
Решение задачи:
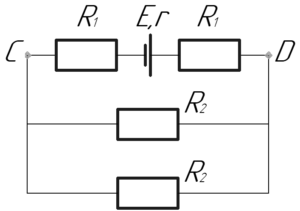 Изображенную в условии задачи электрическую цепь представим в другом виде, смотрите схему, приведенную справа. Здесь \(R_1\) — сопротивление проводника из нихрома, длиной \(r_{рад}\) (т.е. двумя резисторами \(R_1\) мы показали участки от источника до точек C и D), \(R_2\) — сопротивление проводника из нихрома, длиной \({\pi}r_{рад}\) (т.е. двумя резисторами \(R_2\) мы показали участки в виде дуг окружности от точки C до точки D).
Изображенную в условии задачи электрическую цепь представим в другом виде, смотрите схему, приведенную справа. Здесь \(R_1\) — сопротивление проводника из нихрома, длиной \(r_{рад}\) (т.е. двумя резисторами \(R_1\) мы показали участки от источника до точек C и D), \(R_2\) — сопротивление проводника из нихрома, длиной \({\pi}r_{рад}\) (т.е. двумя резисторами \(R_2\) мы показали участки в виде дуг окружности от точки C до точки D).
Понятно, что численные значения сопротивлений \(R_1\) и \(R_2\) можно найти по таким известным формулам:
\[\left\{ \begin{gathered}
{R_1} = \rho \frac{{{r_{рад}}}}{S} \hfill \\
{R_2} = \rho \frac{{\pi {r_{рад}}}}{S} \hfill \\
\end{gathered} \right.\]
В этих формулах \(\rho\) — удельное электрическое сопротивление нихрома, равное 1100 нОм·м.
Учитывая, что два проводника \(R_2\) соединены параллельно, то разность потенциалов между точками C и D можно определить таким образом:
\[U = I\frac{{{R_2}}}{2}\;\;\;\;(1)\]
Силу тока \(I\) в электрической цепи найдем, применив закон Ома для полной цепи:
\[I = \frac{{\rm E}}{{R + r}}\;\;\;\;(2)\]
Здесь \(R\) — полное внешнее сопротивление электрической цепи, которое можно посчитать по такой формуле (поскольку два последовательно соединенных резистора \(R_1\) соединены последовательно с двумя параллельно соединенными резисторами \(R_2\)):
\[R = 2{R_1} + \frac{{{R_2}}}{2}\]
\[R = \frac{{4{R_1} + {R_2}}}{2}\;\;\;\;(3)\]
Подставим (3) в (2):
\[I = \frac{{\rm E}}{{\frac{{4{R_1} + {R_2}}}{2} + r}}\]
\[I = \frac{{2{\rm E}}}{{4{R_1} + {R_2} + 2r}}\]
Это выражение подставим в (1), тогда:
\[U = \frac{{{\rm E}{R_2}}}{{4{R_1} + {R_2} + 2r}}\]
Осталось только использовать формулы для нахождения \(R_1\) и \(R_2\), приведенные в системе:
\[U = \frac{{{\rm E}\rho \frac{{\pi {r_{рад}}}}{S}}}{{4\rho \frac{{{r_{рад}}}}{S} + \rho \frac{{\pi {r_{рад}}}}{S} + 2r}}\]
Домножим и числитель, и знаменатель на \(S\):
\[U = \frac{{{\rm E}\rho \pi {r_{рад}}}}{{4\rho {r_{рад}} + \rho \pi {r_{рад}} + 2rS}}\]
\[U = \frac{{{\rm E}\rho \pi {r_{рад}}}}{{\rho {r_{рад}}\left( {4 + \pi } \right) + 2rS}}\]
Задача решена в общем виде, теперь посчитаем ответ:
\[U = \frac{{2 \cdot 1100 \cdot {{10}^{ — 9}} \cdot 3,14 \cdot 1}}{{1100 \cdot {{10}^{ — 9}} \cdot 1 \cdot \left( {4 + 3,14} \right) + 2 \cdot 1,5 \cdot {{10}^{ — 6}}}} = 0,637\;В = 637\;мВ\]
Ответ: 637 мВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.40 Определите заряд на обкладках конденсатора C=1 мкФ. ЭДС источника 4 В, внутреннее
7.2.42 Указать направление вектора сторонней силы, действующей на положительный заряд q
7.2.43 В конце заряда батареи аккумуляторов током I1 присоединенный к ней вольтметр показывал

 icodepro.ru
icodepro.ru