icodepro.ruУсловие задачи:
Пушка, стоящая на горизонтальной поверхности, стреляет под углом 30° к горизонту. Масса снаряда 20 кг, его начальная скорость 200 м/с. На какое расстояние откатится пушка при выстреле, если её масса 500 кг, а коэффициент сопротивления движению 0,8.
Задача №2.10.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(m=20\) кг, \(\upsilon_0=200\) м/с, \(M=500\) кг, \(\mu=0,8\), \(S-?\)
Решение задачи:
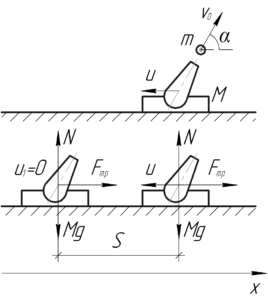На систему «пушка — снаряд» вдоль оси \(x\) не действуют никакие внешние силы, то есть система замкнута. Воспользуемся законом сохранения импульса в проекции на ось \(x\):
\[0 = m{\upsilon _0}\cos \alpha — Mu\]
\[u = \frac{{m{\upsilon _0}\cos \alpha }}{M}\;\;\;\;(1)\]
Приобретя после выстрела скорость \(u\), пушка начнет свое движение, но поскольку поверхность не гладкая, то рано или поздно она остановится из-за силы трения. Согласно теореме об изменении кинетической энергии, работа силы трения равна изменению кинетической энергии:
\[{A_{тр}} = \Delta {E_{к}}\;\;\;\;(2)\]
Силу трения можно найти по следующей формуле (также смотрите рисунок):
\[{F_{тр}} = \mu N = \mu Mg\]
Заметим, что коэффициент сопротивления движению и коэффициент трения — это одно и то же.
Сила трения совершает отрицательную работу, поскольку вектор силы трения противоположен вектору перемещения пушки.
\[{A_{тр}} = — {F_{тр}} \cdot S = — \mu MgS\]
Изменение кинетической энергии, очевидно, равно:
\[\Delta {E_{к}} = 0 — \frac{{M{u^2}}}{2} = — \frac{{M{u^2}}}{2}\]
Тогда равенство (2) примет такой вид:
\[ — \mu MgS = — \frac{{M{u^2}}}{2}\]
\[S = \frac{{M{u^2}}}{{2\mu Mg}} = \frac{{{u^2}}}{{2\mu g}}\]
Учитывая выражение (1) для скорости пушки после выстрела, получим:
\[S = \frac{{{m^2}\upsilon _0^2{{\cos }^2}\alpha }}{{2{M^2}\mu g}}\]
Все данные задачи приведены в системе СИ, поэтому можно приступать к расчету численного ответа.
\[S = \frac{{{{20}^2} \cdot {{200}^2} \cdot {{\cos }^2}30^\circ }}{{2 \cdot {{500}^2} \cdot 0,8 \cdot 10}} = 3\; м\]
Ответ: 3 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.11 На тележку с песком массой 49 кг, движущуюся по прямой со скоростью 1 м/с, падает
2.10.13 Свинцовый шар массой 500 г, движущийся со скоростью 10 м/с, соударяется
2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
Пушка, стоявшая на ровной поверхности, выстрелила под углом ? = 60 ° к земле. Масса пули m = 0,5 кг, а значение ее скорости на выходе из ствола v = 60 м / с. Как далеко она переместится после выстрела, если сила трения между пушкой и землей F = 50 Н? Масса пушки с пулей М = 100 кг.
я нашла коэффициент сопротивления движению: u = F/M*п u = 0,05
S=m^2*v^2*cos^2/2M^ug S = 0.5^2 * 60^2 * cos(60)^2 / 2 * 100^2 * 0.05 * 10 = 9/400 = 0.0225
помогите с ответом, не похоже, что правильно
и нужно ли вычесть из массы пушки массу пули?
Расстояние будем искать по формуле:\[S = \frac{{{u^2}}}{{2a}}\]Ускорение, действующее при откате на пушку, определим из второго закона Ньютона:\[a = \frac{F}{{M — m}}\]Обратите Ваше внимание, что \(M\) — это масса пушки с пулей (корректнее всё-таки говорить снаряд, а не пуля, я считаю). Скорость пушки после выстрела определим из закона сохранения импульса (как и в вышеприведенной задаче):\[u = \frac{{m\upsilon \cos \alpha }}{{M — m}}\]В итоге должны получить такую формулу:\[S = \frac{{{m^2}{\upsilon ^2}{{\cos }^2}\alpha }}{{2F\left( {M — m} \right)}}\]\[S = \frac{{{{0,5}^2} \cdot {{60}^2} \cdot {{\cos }^2}60^\circ }}{{2 \cdot 50 \cdot \left( {100 — 0,5} \right)}} = 0,02261\;м\]
А почему 3?
Смотрите решение выше