Условие задачи:

Ракета летит со скоростью 4 км/с. Затем она движется с постоянным ускорением в течение 1000 с и в последнюю секунду проходит путь 1 км. Определить абсолютную величину ускорения ракеты.

Задача №1.3.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=4\) км/с, \(t=1000\) с, \(S_1=1\) км, \(a-?\)

Решение задачи:

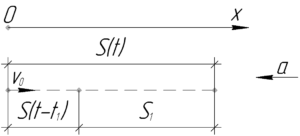Путь за последнюю \(t_1=1\) секунду можно определить, отняв из пути за полное время \(t\) путь за время \(\left( {t — {t_1}} \right)\).

\[{S_1} = S\left( t \right) — S\left( {t — {t_1}} \right)\;\;\;\;(1)\]

Движение тела является равнозамедленным, поэтому запишем соответствующие уравнения движения:

\[S\left( t \right) = {\upsilon _0}t — \frac{{a{t^2}}}{2}\;\;\;\;(2)\]

\[S\left( {t — {t_1}} \right) = {\upsilon _0}\left( {t — {t_1}} \right) — \frac{{a{{\left( {t — {t_1}} \right)}^2}}}{2}\;\;\;\;(3)\]

Подставим выражения (2) и (3) в (1) и раскроем скобки.

\[{S_1} = {\upsilon _0}t — \frac{{a{t^2}}}{2} — \left( {{\upsilon _0}\left( {t — {t_1}} \right) — \frac{{a{{\left( {t — {t_1}} \right)}^2}}}{2}} \right)\]

\[{S_1} = {\upsilon _0}t — \frac{{a{t^2}}}{2} — {\upsilon _0}t + {\upsilon _0}{t_1} + \frac{{a{t^2}}}{2} — at{t_1} + \frac{{at_1^2}}{2}\]

\[{S_1} = {\upsilon _0}{t_1} — at{t_1} + \frac{{at_1^2}}{2}\]

Члены выражения с множителем \(a\) перенесем в левую сторону и вынесем за скобки:

\[a\left( {t{t_1} — \frac{{t_1^2}}{2}} \right) = {\upsilon _0}{t_1} — {S_1}\]

\[\frac{{a\left( {2t{t_1} — t_1^2} \right)}}{2} = {\upsilon _0}{t_1} — {S_1}\]

В итоге:

\[a = \frac{{2\left( {{\upsilon _0}{t_1} — {S_1}} \right)}}{{2t{t_1} — t_1^2}}\]

Подсчитаем численный ответ:

\[a = \frac{{2\left( {4000 \cdot 1 — 1000} \right)}}{{2 \cdot 1000 \cdot 1 — {1^2}}} = 3\; м/с^2\]

Ответ: 3 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.34 На некотором отрезке пути скорость тела увеличилась с 12 см/с до 16 см/с
1.3.36 Тело движется прямолинейно с ускорением 4 м/с2. Начальная скорость тела
1.3.37 Тело движется с начальной скоростью 4 м/с вдоль прямой, причем его скорость