Условие задачи:
Расстояние между двумя опорами 8 м. На эти опоры положили горизонтальную балку массы 100 кг и длины 10 м так, чтобы 2 м балки выступали за левую опору. Чему равна сила давления балки на левую опору?
Задача №3.1.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(l=8\) м, \(M=100\) кг, \(L=10\) м, \(F_1-?\)
Решение задачи:
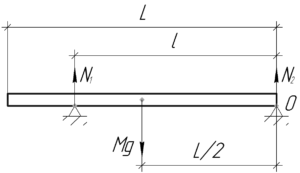 Балка находится в равновесии под действием силы тяжести \(Mg\) и двух сил реакции опоры \(N_1\) и \(N_2\). Давайте найдем величину силы реакции \(N_1\), поскольку она равна по величине искомой силе давления \(F_1\) по третьему закону Ньютона. Для этого запишем второе условие равновесия (правило моментов) относительно точки O:
Балка находится в равновесии под действием силы тяжести \(Mg\) и двух сил реакции опоры \(N_1\) и \(N_2\). Давайте найдем величину силы реакции \(N_1\), поскольку она равна по величине искомой силе давления \(F_1\) по третьему закону Ньютона. Для этого запишем второе условие равновесия (правило моментов) относительно точки O:
\[Mg \cdot \frac{L}{2} — {N_1} \cdot l = 0\]
Откуда:
\[{N_1} = Mg\frac{L}{{2l}}\]
Посчитаем численный ответ к задаче:
\[{N_1} = 100 \cdot 10 \cdot \frac{{10}}{{2 \cdot 8}} = 625\;Н\]
Ответ: 625 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.29 Однородная балка длины 2 м и массы 1000 кг удерживается в горизонтальном положении
3.1.31 С помощью каната, перекинутого через неподвижный блок, укрепленный под потолком
3.1.32 Под каким наименьшим углом a к горизонту может стоять лестница, прислоненная

 icodepro.ru
icodepro.ru
Откуда L/2 по ньютону к 1 опоре? я не понимаю распределения!
Зачем переобозначать реакции опор?