Условие задачи:
 С каким ускорением движутся грузы \(m_1=0,5\) кг и \(m_2=0,6\) кг, если высота наклонной плоскости \(H=60\) см, длина наклонной плоскости \(l=1\) м и коэффициент трения первого груза о плоскость 0,25? Невесомый блок вращается по часовой стрелке.
С каким ускорением движутся грузы \(m_1=0,5\) кг и \(m_2=0,6\) кг, если высота наклонной плоскости \(H=60\) см, длина наклонной плоскости \(l=1\) м и коэффициент трения первого груза о плоскость 0,25? Невесомый блок вращается по часовой стрелке.
Задача №2.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=0,5\) кг, \(m_2=0,6\) кг, \(H=60\) см, \(l=1\) м, \(\mu=0,25\), \(a-?\)
Решение задачи:
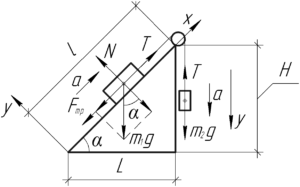 Сделав схему к задаче, введем координатные оси для каждого груза и покажем все силы, действующие на них (смотрите схему). Грузы движутся ускоренно, причем первый груз поднимается по плоскости, а второй — опускается вниз, так как блок вращается по часовой стрелке. Запишем второй закон Ньютона для второго груза в проекции на ось \(y\):
Сделав схему к задаче, введем координатные оси для каждого груза и покажем все силы, действующие на них (смотрите схему). Грузы движутся ускоренно, причем первый груз поднимается по плоскости, а второй — опускается вниз, так как блок вращается по часовой стрелке. Запишем второй закон Ньютона для второго груза в проекции на ось \(y\):
\[{m_2}g — T = {m_2}a\;\;\;\;(1)\]
Для первого груза запишем второй закон Ньютона в проекции на ось \(x\) и первый закон Ньютона в проекции на ось \(y\):
\[\left\{ \begin{gathered}
T — {m_1}g\sin \alpha — {F_{тр}} = {m_1}a \;\;\;\;(2)\hfill \\
N = {m_1}g\cos \alpha \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Силу трения скольжения определяют по следующей формуле:
\[{F_{тр}} = \mu N\]
Так как мы уже определили силу реакции опоры (формула (3)), то:
\[{F_{тр}} = \mu {m_1}g\cos \alpha \]
Полученное подставим в (2), тогда:
\[T — {m_1}g\sin \alpha — \mu {m_1}g\cos \alpha = {m_1}a\;\;\;\;(4)\]
Теперь сложим равенства (1) и (4), в итоге получим:
\[{m_2}g — {m_1}g\sin \alpha — \mu {m_1}g\cos \alpha = \left( {{m_1} + {m_2}} \right)a\;\;\;\;(5)\]
Вы должны заметить, что нам неизвестен угол наклонной плоскости \(\alpha\) и тригонометрические функции этого угла. Но их можно выразить через геометрические параметры наклонной плоскости, что мы сейчас и сделаем. Для начала определим длину основания наклонной плоскости по теореме Пифагора:
\[L = \sqrt {{l^2} — {H^2}} \]
Тогда синус и косинус угла \(\alpha\) по определению равны:
\[\sin \alpha = \frac{H}{l}\]
\[\cos \alpha = \frac{L}{l} = \frac{{\sqrt {{l^2} — {H^2}} }}{l}\]
Полученное подставим в (5), далее домножим обе части равенства на \(l\) и выразим искомое ускорение \(a\):
\[{m_2}g — {m_1}g\frac{H}{l} — \mu {m_1}g\frac{{\sqrt {{l^2} — {H^2}} }}{l} = \left( {{m_1} + {m_2}} \right)a\]
\[{m_2}gl — {m_1}gH — \mu {m_1}g\sqrt {{l^2} — {H^2}} = \left( {{m_1} + {m_2}} \right)al\]
\[a = \frac{{g\left( {{m_2}l — {m_1}H — \mu {m_1}\sqrt {{l^2} — {H^2}} } \right)}}{{\left( {{m_1} + {m_2}} \right)l}}\]
Переведем высоту \(H\) в систему СИ:
\[60\; см = \frac{{60}}{{100}}\; м = 0,6\; м\]
Посчитаем численный ответ:
\[a = \frac{{10 \cdot \left( {0,6 \cdot 1 — 0,5 \cdot 0,6 — 0,25 \cdot 0,5 \cdot \sqrt {{1^2} — {{0,6}^2}} } \right)}}{{\left( {0,5 + 0,6} \right) \cdot 1}} = 1,82\; м/с^2\]
Ответ: 1,82 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами

 icodepro.ru
icodepro.ru
мне кажется, что удобнее было бы выразить косинус через основное тригонометрическое тождество
хотя по ничего в целом не изменится
Именно
Согласен, я тоже решал через cos=?(1-sin^2)
Объясните, пожалуйста, 3 уравнение (которое в системе)- первый закон Ньютона на ось У…при чем тут первый закон, если тело движется с ускорением?
Вдоль оси \(y\) тело не движется, поэтому применяем первый закон Ньютона, а не второй
T—m1gsin?—Fтр=m1a(2)
Что мы выражали через m1gsin? ? Не понимаю зачем оно здесь нужно, какую силу мы через m1gsin? выразили ?
Ничего мы не выражали, это просто проекция силы тяжести первого груза m1g на ось x