Условие задачи:
С вершины холма бросают камень с начальной скоростью \(v_0=10\) м/с под углом \(\alpha=60^\circ\) к горизонту. На каком расстоянии от вершины холма упадет камень, если поверхность холма представляет собой наклонную плоскость с углом \(\beta=45^\circ\) в основании? Рисунок, данный к задаче, изображен справа, кликните по нему для увеличения.
Задача №1.6.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(v_0=10\) м/с, \(\alpha=60^\circ\), \(\beta=45^\circ\), \(L-?\)
Решение задачи:
 Итак, чтобы решить данную непростую задачу по кинематике, необходимо применить одну небольшую хитрость.
Итак, чтобы решить данную непростую задачу по кинематике, необходимо применить одну небольшую хитрость.
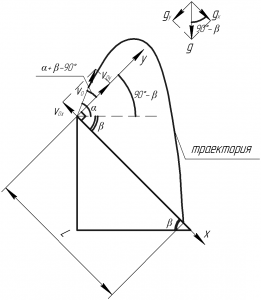
Обычно в задачах на движение тела под углом к горизонту направление осей \(x\) и \(y\) берется как обычно, т.е. перпендикулярно и параллельно поверхности земли соответственно. Но если в этой задаче вводить оси таким же образом, то она станет сложнее для решения, поэтому ось \(y\) направим перпендикулярно плоскости холма, а ось \(x\) — по холму, как вы можете видеть на рисунке (кликните по нему для увеличения).
Теперь разберемся с углами, поскольку они необходимы для правильного проецирования начальной скорости и ускорения свободного падения (да, в этой задаче нужно проецировать и ее).
Во-первых, угол между холмом и вектором начальной скорости \(v_0\) равен \(\alpha+\beta\), поэтому угол между вектором начальной скорости \(v_0\) и осью \(y\) равен \(\alpha+\beta — 90^\circ\).
Во-вторых, угол между проекцией вектора начальной скорости \(v_{0y}\) и горизонтом равен \(\alpha — (\alpha+\beta — 90^\circ)\), т.е. \(90^\circ — \beta\). Этот же угол имеет место между вектором ускорения свободного падения \(g\) и его проекцией на ось \(x\) \(g_x\).
Осталось только написать уравнения движения в проекциях на обе оси и решить их.
\[\left\{ \begin{gathered}
oy:\,\,y = {v_0}\cos \left( {\alpha + \beta — 90^\circ } \right)t — \frac{{g\sin \left( {90^\circ — \beta } \right){t^2}}}{2}\,\,\,\,\,\,\,\,(1) \hfill \\
ox:\,\,x = — {v_0}\sin \left( {\alpha + \beta — 90^\circ } \right)t + \frac{{g\cos \left( {90^\circ — \beta } \right){t^2}}}{2}\,\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Примечательно, что движение по обоим осям, даже по оси \(x\), является ускоренным.
В момент касания камня о холм, его координата \(y\) будет равна нулю, поэтому приравняем уравнение (1) к нулю.
\[y = 0 \Rightarrow {v_0}\cos \left( {\alpha + \beta — 90^\circ } \right)t — \frac{{g\sin \left( {90^\circ — \beta } \right){t^2}}}{2} = 0\]
Решая данное уравнение получаем 2 корня:
\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{v_0}\cos \left( {\alpha + \beta — 90^\circ } \right)}}{{g\sin \left( {90^\circ — \beta } \right)}} \hfill \\
\end{gathered} \right.\]
Первый корень \(t = 0\) соответствует моменту бросания камня и нам не нужен. Осталось подставить второй корень в уравнение (2), произвести тригонометрические преобразования и получить ответ в общем виде.
\[L = \frac{{v_0^2\sin \left( {2\alpha + 2\beta } \right)}}{{g\cos \left( \beta \right)}} + \frac{{2v_0^2\sin \left( \beta \right){{\sin }^2}\left( {\alpha + \beta } \right)}}{{g{{\cos }^2}\left( \beta \right)}}\]
Подставим все исходные данные в СИ и получим ответ.
\[L = \frac{{{{10}^2} \cdot \sin \left( {2 \cdot 60^\circ + 2 \cdot 45^\circ } \right)}}{{10 \cdot \cos \left( {45^\circ } \right)}} + \frac{{2 \cdot {{10}^2} \cdot \sin \left( {45^\circ } \right){{\sin }^2}\left( {60^\circ + 45^\circ } \right)}}{{10 \cdot {{\cos }^2}\left( {45^\circ } \right)}} = 19,32\; м.\]
Ответ: 19,32 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.19 Какой скоростью обладал мальчик при прыжке с трамплина
1.6.21 Струя воды бьет под углом 32 градуса к горизонту. На расстоянии
1.6.22 Тело брошено под углом 60 к горизонту с начальной скоростью

 icodepro.ru
icodepro.ru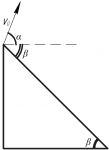
Как можно принимать координату y=0 во время падения, если y=0 в самом начале, в момент броска?
В моей введенной системе координат так и будет, смотрите рисунок
Почему по Оси X начальная скорость со знаком «-«?
Потому что v0x противонаправлена оси x
Как вышло
Что по оси Х будет sina
А по оси У cosa?
На рисунке я показал как проецирую начальную скорость на оси координат x и y.
Если Вы умеете проецировать вектора на оси координат, то посмотрев на рисунок, Вы сразу все поймете.