Условие задачи:
Сани массы 300 кг равномерно движутся по горизонтальной снежной поверхности. Температура снега равна 0 °C, коэффициент трения полозьев саней о снег равен 0,033. Сколько снега расплавится под полозьями саней на пути в 1 км, если всё количество теплоты от трения идёт на плавление снега?
Задача №5.3.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(M=300\) кг, \(t_0=0^\circ\) C, \(\mu=0,033\), \(S=1\) км, \(m-?\)
Решение задачи:
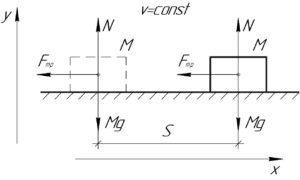 Количество теплоты \(Q\), необходимое для плавления снега искомой массы \(m\), равно модулю работы силы трения скольжения \(A_{тр}\), действующей на сани.
Количество теплоты \(Q\), необходимое для плавления снега искомой массы \(m\), равно модулю работы силы трения скольжения \(A_{тр}\), действующей на сани.
\[Q = \left| {{A_{тр}}} \right|\;\;\;\;(1)\]
Понятно, что указанное количество теплоты \(Q\) можно определить по формуле:
\[Q = \lambda m\;\;\;\;(2)\]
Здесь \(\lambda\) — удельная теплота плавления снега, равная 330 кДж/кг.
Модуль (то есть абсолютную величину) работы силы трения скольжения найдём по формуле:
\[\left| {{A_{тр}}} \right| = {F_{тр}}S\]
Саму силу трения скольжения найдём следующим образом (\(N=Mg\) по первому закону Ньютона в проекции на ось \(y\)):
\[{F_{тр}} = \mu N = \mu Mg\]
Тогда:
\[\left| {{A_{тр}}} \right| = \mu MgS\;\;\;\;(3)\]
Подставим выражения (2) и (3) в равенство (1):
\[\lambda m = \mu MgS\]
\[m = \frac{{\mu MgS}}{\lambda }\]
Задача решена в общем виде, теперь посчитаем численный ответ:
\[m = \frac{{0,033 \cdot 300 \cdot 10 \cdot {{10}^3}}}{{330 \cdot {{10}^3}}} = 0,3\;кг\]
Ответ: 0,3 кг.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.3.20 Железный метеорит влетает в атмосферу Земли со скоростью 1,5·103 м/с
5.3.22 Найти работу газа, совершенную в процессе 1-2-3
5.3.23 Найти работу газа в процессе 1-2-3

 icodepro.ru
icodepro.ru
Благодарю
