Условие задачи:

Шарик на нити, уравновешенный на весах, опускают в воду. Когда шарик на 0,3 своего объема погрузился в воду, равновесие нарушилось и для его восстановления пришлось снять гирьки, масса которых составила 1/6 часть массы шарика. Какова плотность материала шарика?

Задача №3.3.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$V_п=0,3V$, $\Delta m = \frac{1}{6}m$, $\rho-?$

Решение задачи:

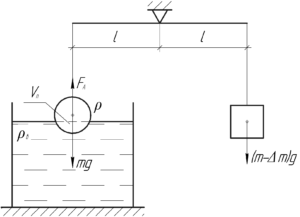Должно быть понятно, что равновесие возможно лишь в том случае, когда на левое и правое плечо весов действуют одинаковые силы (вообще моменты силы, но в данном случае плечи, очевидно, равны). Поэтому:

$$mg — {F_А} = \left( {m — \Delta m} \right)g$$

$$\Delta mg = {F_А}$$

По условию $\Delta m = \frac{1}{6}m$, значит:

$$\frac{1}{6}mg = {F_А}$$

Запишем массу шарика $m$ как произведение плотности $\rho$ на полный объем $V$, а силу Архимеда через известную формулу её определения:

$$\frac{1}{6}\rho Vg = {\rho _в}g{V_п}$$

$$\frac{1}{6}\rho V = {\rho _в}{V_п}$$

По условию шарик погружен в жидкость на 0,3 своего объема ($V_п=0,3V$), поэтому:

$$\frac{1}{6}\rho V = 0,3{\rho _в}V$$

$$\rho  = 1,8{\rho _в}$$

Плотность воды $\rho_в$ равна 1000 кг/м³. Значит плотность материала шарика $\rho$ равна:

$$\rho  = 1,8 \cdot 1000 = 1800\;кг/м^3$$

Ответ: 1800 кг/м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.30 Шарик массой 20 г всплывает с постоянной скоростью в жидкости, плотность которой
3.3.32 В сосуд налили ртуть и сверху неё масло. Шар в сосуде плавает так, что он ровно
3.3.33 Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде