Условие задачи:
Свинцовая пуля массой 10 г, летящая горизонтально со скоростью 100 м/с, попадает в деревянный брусок массой 1 кг, подвешенный на длинной нити. На сколько градусов нагрелась пуля, если 70% выделенной при ударе теплоты пошло на её нагревание?
Задача №5.3.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10\) г, \(\upsilon=100\) м/с, \(M=1\) кг, \(\alpha=70\%\), \(\Delta t-?\)
Решение задачи:
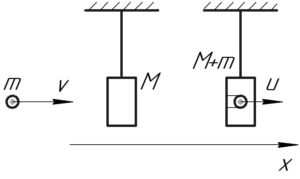 Так как в условии не говорится о том, что пуля пройдёт насквозь через деревянный брусок, значит всё-таки пуля застряла в бруске. Получается, что имеет место абсолютно неупругий удар (а это значит, что часть кинетической энергии перейдёт во внутреннюю). Пусть \(u\) — скорость бруска после попадания (вместе с пулей). Запишем закон сохранения импульса (ЗСИ) в проекции на ось \(x\):
Так как в условии не говорится о том, что пуля пройдёт насквозь через деревянный брусок, значит всё-таки пуля застряла в бруске. Получается, что имеет место абсолютно неупругий удар (а это значит, что часть кинетической энергии перейдёт во внутреннюю). Пусть \(u\) — скорость бруска после попадания (вместе с пулей). Запишем закон сохранения импульса (ЗСИ) в проекции на ось \(x\):
\[m\upsilon = \left( {m + M} \right)u\]
Откуда:
\[u = \frac{{m\upsilon }}{{m + M}}\;\;\;\;(1)\]
Теперь запишем закон сохранения энергии (ЗСЭ):
\[\frac{{m{\upsilon ^2}}}{2} = \frac{{\left( {m + M} \right){u^2}}}{2} + Q\]
Подставим выражение (1) в полученное уравнение:
\[\frac{{m{\upsilon ^2}}}{2} = \frac{{\left( {m + M} \right){m^2}{\upsilon ^2}}}{{2{{\left( {m + M} \right)}^2}}} + Q\]
\[\frac{{m{\upsilon ^2}}}{2} = \frac{{{m^2}{\upsilon ^2}}}{{2\left( {m + M} \right)}} + Q\]
Выразим количество теплоты \(Q\), выделившееся при ударе:
\[Q = \frac{{m{\upsilon ^2}}}{2} — \frac{{{m^2}{\upsilon ^2}}}{{2\left( {m + M} \right)}} = \frac{{m{\upsilon ^2}\left( {m + M} \right) — {m^2}{\upsilon ^2}}}{{2\left( {m + M} \right)}}\]
\[Q = \frac{{mM{\upsilon ^2}}}{{2\left( {m + M} \right)}}\;\;\;\;(2)\]
Обратите внимание, что лишь \(\alpha\) часть количества теплоты \(Q\) пошла на нагревание пули (остальная часть могла, например, пойти на нагревание бруска):
\[{Q_1} = \alpha Q\;\;\;\;(3)\]
Количество теплоты \(Q_1\), необходимое для изменения температуры пули на величину \(\Delta t\), также определим по формуле:
\[{Q_1} = cm\Delta t\;\;\;\;(4)\]
Удельная теплоёмкость свинца \(c\) равна 130 Дж/(кг·°C).
Учитывая (3) и (4), имеем:
\[cm\Delta t = \alpha Q\]
Подставим в полученное равенство выражение (2):
\[cm\Delta t = \frac{{\alpha mM{\upsilon ^2}}}{{2\left( {m + M} \right)}}\]
\[c\Delta t = \frac{{\alpha M{\upsilon ^2}}}{{2\left( {m + M} \right)}}\]
\[\Delta t = \frac{{\alpha M{\upsilon ^2}}}{{2c\left( {m + M} \right)}}\]
Переведём массу пули \(m\) в килограммы, а величину \(\alpha\) — в доли единицы:
\[10\;г = 0,01\;кг\]
\[70\% = 0,7\]
Посчитаем численный ответ задачи:
\[\Delta t = \frac{{0,7 \cdot 1 \cdot {{100}^2}}}{{2 \cdot 130 \cdot \left( {0,01 + 1} \right)}} = 26,7^\circ\;C = 26,7\;К\]
Ответ: 26,7 К.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.3.13 Стальной шар, падая свободно, достиг скорости 41 м/с и, ударившись о землю
5.3.15 Свинцовая пуля, летящая со скоростью 430 м/с, пробивает стену, причем скорость
5.3.16 При выстреле вертикально вверх свинцовая пуля ударилась о неупругое тело

 icodepro.ru
icodepro.ru
Кельвин не правильно записали?
а если бы пуля отскочила что бы изменилась?
Закон сохранения импульса и энергии приняли бы другой вид.
Нужна конкретная задача, чтобы на её примере показать решение, разглагольствовать же об этом без конкретной задачи не имеет смысла.