Условие задачи:
Свободно падающий камень пролетел последние три четверти пути за одну секунду. С какой высоты падал камень, если его начальная скорость равна нулю? Сопротивление воздуха не учитывать.
Задача №1.4.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t_1=1\) с, \(S_1=\frac{3H}{4}\), \(\upsilon_0=0\) м/с, \(H-?\)
Решение задачи:
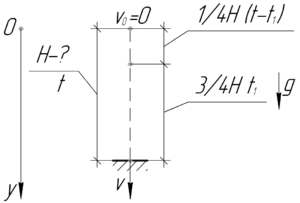 Если тело пролетает весь путь \(H\) за \(t\) секунд, то первую четверть пути \(\frac{1}{4}H\) — за \(\left( {t — {t_1}} \right)\) секунд, поскольку последние три четверти пути \(\frac{3}{4}H\) тело проходит за \(t_1=1\) секунду.
Если тело пролетает весь путь \(H\) за \(t\) секунд, то первую четверть пути \(\frac{1}{4}H\) — за \(\left( {t — {t_1}} \right)\) секунд, поскольку последние три четверти пути \(\frac{3}{4}H\) тело проходит за \(t_1=1\) секунду.
Так как начальная скорость камня \(\upsilon_0\) отсутствует, то запишем следующую систему.
\[\left\{ \begin{gathered}
H = \frac{{g{t^2}}}{2} \hfill \\
\frac{1}{4}H = \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]
Поделим верхнее выражение на нижнее.
\[{\left( {\frac{t}{{t — {t_1}}}} \right)^2} = 4\]
Извлечем квадратный корень из обеих частей равенства. В общем случае, извлекая корень, Вы должны писать следующую совокупность:
\[\left[ \begin{gathered}
\frac{t}{{t — {t_1}}} = 2 \hfill \\
\frac{t}{{t — {t_1}}} = — 2 \hfill \\
\end{gathered} \right.\]
Мы откинули нижнее равенство, поскольку отношение времен \(t\) и \(\left( {t — {t_1}} \right)\) явно должно быть положительным.
\[\frac{t}{{t — {t_1}}} = 2\]
\[t = 2t — 2{t_1}\]
\[t = 2{t_1}\]
Подставим это выражение в первую формулу приведенной системы.
\[H = \frac{{g \cdot 4t_1^2}}{2}\]
\[H = 2gt_1^2\]
Последнее действие — сосчитать численный ответ.
\[H = 2 \cdot 10 \cdot {1^2} = 20\; м \]
Ответ: 20 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.42 При падении камня в колодец его удар о поверхность воды доносится через 5 с
1.4.44 Тело начинает свободно падать с высоты 45 м. В тот же момент с высоты 24 м
1.4.45 Тело падает без начальной скорости с высоты 45 м. Определить среднюю скорость

 icodepro.ru
icodepro.ru