Условие задачи:

Тележка движется по горизонтальной поверхности со скоростью 0,5 м/с. Её догоняет вторая, движущаяся со скоростью 1,5 м/с. После удара обе тележки движутся в том же направлении с одинаковой скоростью 1 м/с. Найти отношение массы второй тележки к массе первой.

Задача №2.10.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=0,5\) м/с, \(\upsilon_2=1,5\) м/с, \(u=1\) м/с, \(\frac{m_2}{m_1}-?\)

Решение задачи:

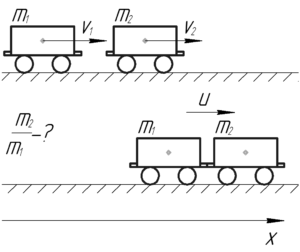Система, состоящая из двух тележек, при отсутствии сил трения является замкнутой вдоль горизонтальной оси, поскольку в этом направлении на тележки не действуют силы. Это даёт нам возможность воспользоваться законом сохранения импульса (также в проекции на горизонтальную ось):

\[{m_1}{\upsilon _1} + {m_2}{\upsilon _2} = {m_1}u + {m_2}u\]

Так как нам необходимо найти в задаче отношение масс, то поделим обе части получившегося равенства на \(m_1\).

\[{\upsilon _1} + \frac{{{m_2}}}{{{m_1}}}{\upsilon _2} = u + \frac{{{m_2}}}{{{m_1}}}u\]

Перенесем все члены с множителем \(\frac{m_2}{m_1}\) в правую сторону, остальные — в левую.

\[\frac{{{m_2}}}{{{m_1}}}{\upsilon _2} — \frac{{{m_2}}}{{{m_1}}}u = u — {\upsilon _1}\]

Вынесем \(\frac{m_2}{m_1}\) за скобки:

\[\frac{{{m_2}}}{{{m_1}}}\left( {{\upsilon _2} — u} \right) = u — {\upsilon _1}\]

В конце концов получаем следующую итоговую формулу:

\[\frac{{{m_2}}}{{{m_1}}} = \frac{{u — {\upsilon _1}}}{{{\upsilon _2} — u}}\]

Подставляем числа в формулу, считаем ответ:

\[\frac{{{m_2}}}{{{m_1}}} = \frac{{1 — 0,5}}{{1,5 — 1}} = 1\]

Получается, что массы тележек равны между собой.

Ответ: 1.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.14 Стоящий на льду человек массой 60 кг ловит мяч массой 0,5 кг, который летит
2.10.16 Конькобежец, стоя на льду, бросил вперед гирю массой 5 кг и вследствие отдачи
2.10.17 Два мальчика играют в мяч, стоя на льду на расстоянии 10 м друг от друга