Условие задачи:
Тело, двигаясь равноускоренно, проходит 80 м за 4 с. Чему равна мгновенная скорость в момент времени 1 с, \(\upsilon_0=0\).
Задача №1.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=80\) м, \(t=4\) с, \(\upsilon_0=0\) м/с, \(t_1=1\) с, \(\upsilon-?\)
Решение задачи:
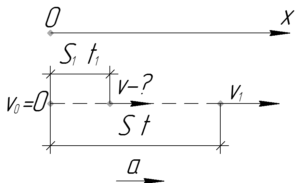 Если тело движется без начальной скорости, т.е. \(\upsilon_0=0\), то пройденный им за время \(t\) путь легко найти из формулы:
Если тело движется без начальной скорости, т.е. \(\upsilon_0=0\), то пройденный им за время \(t\) путь легко найти из формулы:
\[S = \frac{{a{t^2}}}{2}\]
Найдем из этой формулы ускорение \(a\).
\[a = \frac{{2S}}{{{t^2}}}\]
В случае равноускоренного движения скорость определяется из следующего выражения:
\[\upsilon = {\upsilon _0} + at\]
Как уже было сказано \(\upsilon_0=0\). Так как нам необходимо найти скорость в момент времени \(t_1\), то выражение примет вид:
\[\upsilon = a{t_1}\]
Подставим сюда полученную нами формулу для ускорения, тогда получим итоговую формулу:
\[\upsilon = \frac{{2S \cdot {t_1}}}{{{t^2}}}\]
Осталось вычислить ответ, подставив числа в дробь.
\[\upsilon = \frac{{2 \cdot 80 \cdot 1}}{{{4^2}}} = 10\; м/с = 36\; км/ч\]
Ответ: 36 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.7 Движение тела задано уравнением S=40t-0,2t^2. Через какое время
1.3.9 Поезд начинает равноускоренное движение и через 10 с имеет скорость 8 м/с
1.3.10 Мотоциклист, подъезжая к уклону, имеет скорость 10 м/с и начинает двигаться

 icodepro.ru
icodepro.ru
я вначале нашел конечную скорость -> Vк=S/t=80/4=20 м/с
потом нашел ускорение -> a= (Vк-Vо)/t = (20-0)/4= 5 м/с^2
затем просто умножил 1 сек на ускорение и получил скорость=5 м/с , а не 10
Вопрос: где у меня ошибка или изначально что то не так?
В первой же строчке ошибка. Тело движется равноускоренно, а Вы применяете формулу пути для равномерного движения.
Почему вышло 10 м/с если по идеи 20, не?
А по какой идее? Просто разделив 80 м на 4 с?
Движение тела не равномерное, а равноускоренное (об этом явно сказано в условии), поэтому так решать нельзя. Каждую секунду у тела разная скорость.