Условие задачи:

Тело, двигаясь с начальной скоростью 10 м/с и постоянным ускорением 10 м/с², потеряло 75% своей начальной скорости. Какой путь прошло тело за это время?

Задача №1.3.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=10\) м/с, \(a=10\) м/с², \(\alpha=75\)%, \(S-?\)

Решение задачи:

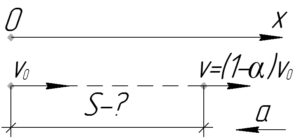Если тело потеряло \(\alpha\) процентов своей начальной скорости, то оно будет иметь в конце пути следующую скорость:

\[\upsilon  = \left( {1 — \alpha } \right){\upsilon _0}\;\;\;\;(1)\]

Вспомним следующую формулу из кинематики:

\[{\upsilon ^2} — \upsilon _0^2 =  — 2aS\;\;\;\;(2)\]

Минус присутствует в правой части формулы из-за того, что движение замедленное. Подставим выражение (1) в формулу (2).

\[{\left( {1 — \alpha } \right)^2}\upsilon _0^2 — \upsilon _0^2 =  — 2aS\]

Произведем математические преобразования, чтобы в конечном итоге найти путь \(S\).

\[\upsilon _0^2\left( {1 — {{\left( {1 — \alpha } \right)}^2}} \right) = 2aS\]

\[\upsilon _0^2\left( {1 — 1 + 2\alpha  — {\alpha^2}} \right) = 2aS\]

\[S = \frac{{\alpha \upsilon _0^2\left( {2 — \alpha} \right)}}{{2a}}\]

Мы получили ответ в общем виде. Подставим числа в формулу, и сосчитаем ответ.

\[S = \frac{{0,75 \cdot {{10}^2}\left( {2 — 0,75} \right)}}{{2 \cdot 10}} = 4,69\; м\]

Ответ: 4,69 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.45 По наклонной доске пустили снизу вверх шарик. На расстоянии 30 см от начала
1.3.47 Тело, имея начальную скорость 1 м/с, двигаясь равноускоренно, приобрело
1.3.48 Прямолинейное движение точки задано уравнением x=-2+3t-0,5t^2 (м). Найти