Условие задачи:

Тело падает без начальной скорости с высоты 45 м. Определить среднюю скорость падения на второй половине пути.

Задача №1.4.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(H=45\) м, \(S_1=\frac{1}{2}H\), \(\upsilon_{ср}-?\)

Решение задачи:

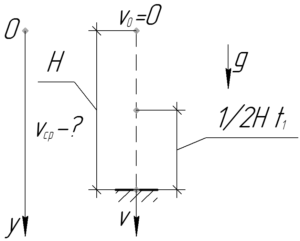Чтобы определить среднюю скорость на второй половине пути, необходимо поделить пройденный путь, равный \(\frac{1}{2}H\), на время \(t_1\), сколько летело тело эту половину пути.

\[{\upsilon _{ср}} = \frac{H}{{2{t_1}}}\]

Найдем время \(t_1\). Для этого воспользуемся следующими рассуждениями. Если тело прошло весь путь \(H\) за время \(t\), а последнюю половину пути за \(t_1\) секунд, то первую половину пути \(\frac{1}{2}H\) оно прошло за \(\left( {t — {t_1}} \right)\). Так как тело двигалось без начальной скорости с ускорением \(g\), то верно записать следующую систему:

\[\left\{ \begin{gathered}
H = \frac{{g{t^2}}}{2} \hfill \\
\frac{1}{2}H = \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]

Поделим верхнее выражение в системе на нижнюю.

\[{\left( {\frac{t}{{t — {t_1}}}} \right)^2} = 2\]

Извлечем квадратный корень из обеих частей равенства.

\[\left[ \begin{gathered}
\frac{t}{{t — {t_1}}} = \sqrt 2 \hfill \\
\frac{t}{{t — {t_1}}} = — \sqrt 2 \hfill \\
\end{gathered} \right.\]

Второе выражение можно «выкинуть», так как очевидно, что отношение времен не может быть отрицательным.

\[t = \sqrt 2 t — \sqrt 2 {t_1}\]

\[{t_1} = t\frac{{\sqrt 2  — 1}}{{\sqrt 2 }}\]

Полное время падения \(t_1\) тела найдем из первой формулы приведенной системы.

\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}} \]

Значит:

\[{t_1} = \frac{{\sqrt 2  — 1}}{{\sqrt 2 }}\sqrt {\frac{{2H}}{g}} \]

В итоге средняя скорость на второй половине пути найдется по формуле:

\[{\upsilon _{ср}} = \frac{{\sqrt 2 H}}{{2\left( {\sqrt 2  — 1} \right)}}\sqrt {\frac{g}{{2H}}} \]

\[{\upsilon _{ср}} = \frac{{\sqrt {gH} }}{{2\left( {\sqrt 2  — 1} \right)}}\]

Подсчитаем численный ответ, используя инженерный калькулятор.

\[{\upsilon _{ср}} = \frac{{\sqrt {10 \cdot 45} }}{{2\left( {\sqrt 2  — 1} \right)}} = 25,61\; м/с = 92,18\; км/ч \]

Ответ: 92,18 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.44 Тело начинает свободно падать с высоты 45 м. В тот же момент с высоты 24 м
1.4.46 Тело свободно падает с высоты 5 м. Найти среднюю скорость тела на нижней
1.4.47 Упругий шар, падая с высоты 80 м, после удара о Землю, отскакивает вертикально