Условие задачи:

Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с^-1. Определить модуль центростремительного ускорения тела.

Задача №1.8.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=2\) м, \(\nu=0,5\) с^-1, \(a_ц-?\)

Решение задачи:

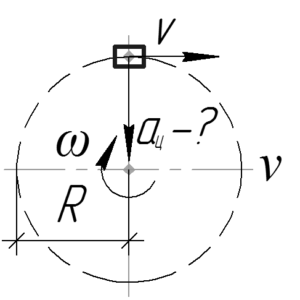Так как ускорение является векторной величиной, то вопрос «определите модуль ускорения» означает что нужно найти его численное значение.

Центростремительное ускорение \(a_ц\) связано с угловой скоростью \(\omega\) и радиусом \(R\) такой формулой:

\[a_ц = {\omega ^2}R\]

Угловая же скорость \(\omega\) связана с данной в условии задачи частотой вращения \(\nu\) другим соотношением:

\[\omega  = 2\pi \nu \]

Подставим это выражение в первую формулу.

\[a_ц = {\left( {2\pi \nu } \right)^2}R\]

\[a_ц = 4{\pi ^2}{\nu ^2}R\]

Дело остается за малым, вычислим численный ответ.

\[a_ц = 4 \cdot {3,14^2} \cdot {0,5^2} \cdot 2 = 19,72\; м/с^2 \approx 20\; м/с^2\]

Ответ: 20 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.12 Тело движется равномерно по окружности. Во сколько раз увеличится
1.8.14 Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его
1.8.15 К валу, радиус которого 5 см, прикреплена нить. Через 5 с после начала равномерного