Условие задачи:
 Точечный источник света освещает тонкий диск диаметром 0,2 м. При этом на экране, расположенном параллельно диску на расстоянии 1 м от него, образуется тень диаметром 0,6 м. Определите расстояние от источника света до экрана.
Точечный источник света освещает тонкий диск диаметром 0,2 м. При этом на экране, расположенном параллельно диску на расстоянии 1 м от него, образуется тень диаметром 0,6 м. Определите расстояние от источника света до экрана.
Задача №10.1.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=0,2\) м, \(b=1\) м, \(D=0,6\) м, \(a-?\)
Решение задачи:
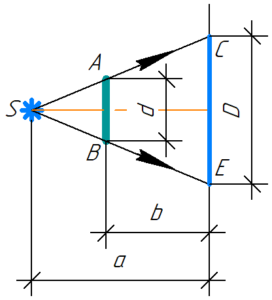 Сделаем рисунок для решения этой задачи, на котором покажем область геометрической тени и все данные в условии размеры.
Сделаем рисунок для решения этой задачи, на котором покажем область геометрической тени и все данные в условии размеры.
Понятно, что треугольники SAB и SCE подобны по трем углам, поэтому справедливо записать:
\[\frac{d}{D} = \frac{{a — b}}{a}\]
Перемножим «крест-накрест»:
\[ad = D\left( {a — b} \right)\]
Раскроем скобки в правой части:
\[ad = Da — Db\]
Перенесем все члены с искомой \(a\) в левую сторону и вынесем её за скобки:
\[ad — Da = — Db\]
\[a\left( {d — D} \right) = — Db\]
\[a\left( {D — d} \right) = Db\]
Окончательно получим такое решение задачи в общем виде:
\[a = \frac{{Db}}{{D — d}}\]
Численный ответ задачи равен:
\[a = \frac{{0,6 \cdot 1}}{{0,6 — 0,2}} = 1,5\;м\]
Ответ: 1,5 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.1.16 Предмет находится от плоского зеркала на расстоянии 30 см. На каком расстоянии
10.1.18 На каком из приведенных ниже рисунков правильно построено изображение И предмета П
10.1.19 Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой

 icodepro.ru
icodepro.ru