Условие задачи:

Тормозной путь автомобиля, двигавшегося со скоростью 30 км/ч, равен 7,2 м. Чему будет равен тормозной путь, если скорость увеличится до 50 км/ч?

Задача №1.3.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=30\) км/ч, \(S_1=7,2\) м, \(\upsilon_2=50\) км/ч, \(S_2-?\)

Решение задачи:

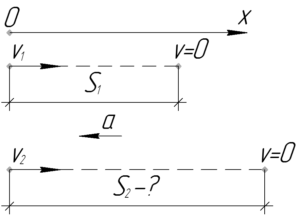Вспомним так называемую формулу кинематики без времени, в общем случае она принимает следующий вид:

\[{\upsilon ^2} — \upsilon _0^2 =  — 2aS\]

Здесь \(\upsilon\) — конечная скорость, которая в нашей задаче в обоих случаях равна нулю, \(\upsilon_0\) — начальная скорость (\(\upsilon_1\) и \(\upsilon_2\)) в нашем случае, \(a\) — модуль ускорения, \(S\) — тормозной путь. «Минус» в правой части учитывает, что движение является замедленным.

Ускорение \(a\) зависит от коэффициента трения поверхности \(\mu\) и ускорения свободного падения \(g\), поэтому в обоих случаях будет одним и тем же.

Учитывая все вышесказанное, запишем систему для двух случаев, описанных в задаче:

\[\left\{ \begin{gathered}
\upsilon _1^2 = 2a{S_1} \hfill \\
\upsilon _2^2 = 2a{S_2} \hfill \\
\end{gathered} \right.\]

Разделим одно выражение системы на другое и выразим искомое \(S_2\).

\[\frac{{{S_2}}}{{{S_1}}} = \frac{{\upsilon _2^2}}{{\upsilon _1^2}} \Rightarrow {S_2} = {S_1}\frac{{\upsilon _2^2}}{{\upsilon _1^2}}\]

Остается вычислить ответ. Заметим, что можно не переводить значения скоростей \(\upsilon_1\) и \(\upsilon_2\) в систему СИ, поскольку в формуле фигурирует их отношение, а оно не меняется при переходе (вы можете сами проверить этот факт).

\[{S_2} = 7,2\frac{{{{50}^2}}}{{{{30}^2}}} = 20\; м \]

Ответ: 20 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.22 Теплоход, двигаясь равноускоренно из состояния покоя с ускорением 0,10 м/с2
1.3.24 Скорость движения автомобиля от времени задана уравнением v=3+2t. Какой
1.3.25 По одному направлению из одной точки одновременно начали двигаться два тела