Условие задачи:
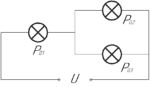 Три лампочки мощностью \(P_{01}=50\) Вт и \(P_{02}=25\) Вт и \(P_{03}=50\) Вт, рассчитанные на напряжение \(U_0=100\) В каждая, соединены, как показано на рисунке, и включены в сеть напряжением \(U=200\) В. Определить мощность, выделяющуюся в первой лампочке.
Три лампочки мощностью \(P_{01}=50\) Вт и \(P_{02}=25\) Вт и \(P_{03}=50\) Вт, рассчитанные на напряжение \(U_0=100\) В каждая, соединены, как показано на рисунке, и включены в сеть напряжением \(U=200\) В. Определить мощность, выделяющуюся в первой лампочке.
Задача №7.4.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(P_{01}=50\) Вт, \(P_{02}=25\) Вт, \(P_{03}=50\) Вт, \(U_0=100\) В, \(U=200\) В, \(P_1-?\)
Решение задачи:
 Зная номинальные мощности и напряжения лампочек (т.е. мощность и напряжение, на которые рассчитаны лампочки), найдем сопротивление каждой лампочки следующим образом:
Зная номинальные мощности и напряжения лампочек (т.е. мощность и напряжение, на которые рассчитаны лампочки), найдем сопротивление каждой лампочки следующим образом:
\[{P_0} = \frac{{U_0^2}}{R} \Rightarrow R = \frac{{U_0^2}}{{{P_0}}}\]
Применительно к каждой лампочке эта формула примет вид:
\[\left\{ \begin{gathered}
{R_1} = \frac{{U_0^2}}{{{P_{01}}}} \hfill \\
{R_2} = \frac{{U_0^2}}{{{P_{02}}}} \hfill \\
{R_3} = \frac{{U_0^2}}{{{P_{03}}}} \hfill \\
\end{gathered} \right.\]
Не будем пытаться решить эту задачу в общем виде (поскольку решение получится очень громоздким), поэтому сразу посчитаем значения сопротивлений:
\[\left\{ \begin{gathered}
{R_1} = \frac{{{{100}^2}}}{{50}} = 200\;Ом \hfill \\
{R_2} = \frac{{{{100}^2}}}{{25}} = 400\;Ом \hfill \\
{R_3} = \frac{{{{100}^2}}}{{50}} = 200\;Ом \hfill \\
\end{gathered} \right.\]
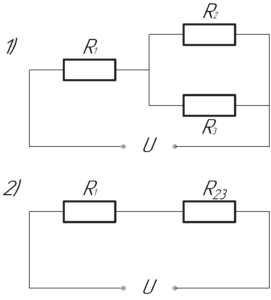
Таким образом мы имеем следующую схему (смотрите рисунок 1 на схеме к решению). Чтобы найти общее сопротивление цепи \(R\), сначала найдем эквивалентное сопротивление \(R_{23}\) соединенных параллельно лампочек 2 и 3 по формуле:
\[R_{23} = \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}}\]
\[R_{23} = \frac{{400 \cdot 200}}{{400 + 200}} = \frac{{400}}{3}\;Ом\]
Тогда общее сопротивление цепи \(R\) равно (как сопротивление двух последовательно соединенных сопротивлений \(R_1\) и \(R_{23}\), смотрите рисунок 2 на схеме к решению):
\[R = {R_1} + {R_{23}}\]
\[R = 200 + \frac{{400}}{3} = \frac{{1000}}{3}\;Ом\]
Силу тока в цепи \(I\) найдем по закону Ома:
\[I = \frac{U}{R}\]
\[I = \frac{{200 \cdot 3}}{{1000}} = 0,6\;А\]
В итоге, мощность \(P_1\), выделяющаяся на первой лампочке, равна:
\[{P_1} = {I^2}{R_1}\]
\[{P_1} = {0,6^2} \cdot 200 = 72\;Вт\]
Комментатор с ником «Mypka» обратил внимание на тот странный факт, что, судя по расчетам, напряжение на первой лампочке равно 120 В, хотя лампа рассчитана на напряжение 100 В. Это говорит о том, что она должна перегореть, то есть ни о какой мощности, выделяющейся в первой лампочке, не может быть и речи. Возможно автор совершил ошибку в численных данных задачи, но сказать об этом точно я не могу. Если Вы будете сдавать эту задачу учителю, лучше сообщите ему об этом факте.
Ответ: 72 Вт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.4.40 Батарея состоит из параллельно соединенных источников тока. При силе тока во внешней цепи
7.4.42 К источнику тока подключен реостат. При сопротивлении реостата 4 Ом и 9 Ом получается
7.4.43 Определить ЭДС аккумулятора, если при нагрузке в 5 А он отдает во внешнюю цепь 10 Вт

 icodepro.ru
icodepro.ru
Лампочки рассчитаны на напряжение 100В каждая, а если силу тока I (0,6 A) «умножить» на сопротивление R1 (200 Ом), то получится 120 В, что превышает допустимое значение лампы, или я не прав?
Хм, похоже, что Вы правы, я добавлю этот факт в решение
Спасибо за решение
решение в одну строчку 400*200 /400+200= 80000/600= 133 ома+ 200 ом=333ома общееR I= U/R = 200/333=0.6
P1=I2R1
Интересно, если я бы представил решение в таком виде, кто-нибудь что-нибудь бы понял?)