Условие задачи:
Цепь состоит из аккумулятора с внутренним сопротивлением 5 Ом и нагрузки 15 Ом. При подключении к нагрузке некоторого резистора параллельно, а затем последовательно ток через этот резистор не меняется. Чему равно сопротивление резистора?
Задача №7.2.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(r=5\) Ом, \(R_0=15\) Ом, \(I_1=I_2\), \(R-?\)
Решение задачи:
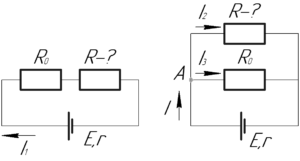 При последовательном подключении нагрузки \(R_0\) с резистором \(R\) ток в цепи можно найти, используя закон Ома для полной цепи, по такой формуле:
При последовательном подключении нагрузки \(R_0\) с резистором \(R\) ток в цепи можно найти, используя закон Ома для полной цепи, по такой формуле:
\[{I_1} = \frac{{\rm E}}{{R + {R_0} + r}}\;\;\;\;(1)\]
Теперь рассмотрим параллельное подключение этих же элементов. Если посмотреть на схему, то в принципе понятно, что в узле A ток \(I\) разделяется на два тока: ток \(I_2\) и ток \(I_3\), поэтому верно (строго говоря, это первый закон Кирхгофа):
\[I = {I_2} + {I_3}\;\;\;\;(2)\]
Так как сопротивления \(R\) и \(R_0\) соединены параллельно (то есть напряжения на них одинаковы), то справедливо равенство:
\[{I_3}{R_0} = {I_2}R\]
Выразим из этого равенства ток \(I_3\):
\[{I_3} = {I_2}\frac{R}{{{R_0}}}\]
Полученное подставим в (2), тогда:
\[I = {I_2} + {I_2}\frac{R}{{{R_0}}}\]
\[I = {I_2}\frac{{{R_0} + R}}{{{R_0}}}\]
Отсюда выразим ток \(I_2\):
\[{I_2} = \frac{{I{R_0}}}{{R + {R_0}}}\;\;\;\;(3)\]
Чтобы узнать ток \(I\), запишем закон Ома для полной цепи:
\[I = \frac{{\rm E}}{{R_{экв} + r}}\;\;\;\;(4)\]
Здесь \(R_{экв}\) — внешнее сопротивление цепи, которое можно найти по формуле (как эквивалентное сопротивление двух параллельно соединенных сопротивлений):
\[{R_{экв}} = \frac{{R{R_0}}}{{R + {R_0}}}\;\;\;\;(5)\]
Подставим (5) в (4):
\[I = \frac{{\text{E}}}{{\frac{{R{R_0}}}{{R + {R_0}}} + r}}\]
Домножим и числитель, и знаменатель на \(\left( {R + {R_0}} \right)\):
\[I = \frac{{{\text{E}}\left( {R + {R_0}} \right)}}{{R{R_0} + r\left( {R + {R_0}} \right)}}\]
\[I = \frac{{{\text{E}}\left( {R + {R_0}} \right)}}{{R{R_0} + rR + r{R_0}}}\]
Полученное подставим в (3), тогда:
\[{I_2} = \frac{{{\text{E}}{R_0}}}{{R{R_0} + rR + r{R_0}}}\;\;\;\;(6)\]
Так как в условии сказано, что при различных вариантах подключения ток через резистор не меняется, то есть \(I_1=I_2\), то приравняем (1) и (6):
\[\frac{{\rm E}}{{R + {R_0} + r}} = \frac{{{\text{E}}{R_0}}}{{R{R_0} + rR + r{R_0}}}\]
\[\frac{1}{{R + {R_0} + r}} = \frac{{{R_0}}}{{R{R_0} + rR + r{R_0}}}\]
Перемножим «крест-накрест»:
\[R{R_0} + R_0^2 + r{R_0} = R{R_0} + rR + r{R_0}\]
\[R_0^2 = rR\]
\[R = \frac{{R_0^2}}{r}\]
Задача решена, посчитаем численный ответ:
\[R = \frac{{{{15}^2}}}{5} = 45\;Ом\]
Ответ: 45 Ом.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.2.27 Батарея элементов замкнута двумя проводниками сопротивлением 4 Ом каждый
7.2.29 Два источника с одинаковыми ЭДС 2 В и внутренними сопротивлениями 0,2 и 0,4 Ом соединены
7.2.30 Источник тока имеет ЭДС 12 В. Сила тока в цепи 4 А, напряжение на внешнем сопротивлении 11 В

 icodepro.ru
icodepro.ru