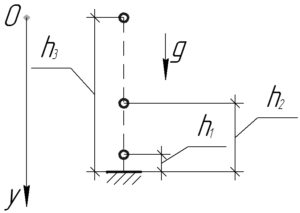
Условие задачи:

Цепочка шаров висит над поверхностью стола: первый шар — на высоте 1 м, второй — на высоте 4 м, третий — на высоте 9 м. Цепочка обрывается, и шары последовательно ударяются об стол. Определите промежутки времени между ударами.

Задача №1.4.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$h_1=1$ м, $h_2=4$ м, $h_3=9$ м, $\tau-?$

Решение задачи:

При рассмотрении задачи шары принимаются материальными точками.

Поскольку между шарами присутствует цепочка, то значит между ними есть кинематическая связь. Из-за этой связи у всех шаров должна быть одинаковая скорость, в противном случае цепочка бы разорвалась и между шарами. Но в данном случае эта связь не усложняет задачу, поскольку тела, итак, в каждый момент времени имеют одинаковые скорости, поскольку падают без начальной скорости с одинаковым ускорением $g$. Значит можно считать, что цепочка между шарами отсутствует. Тогда легко определить через какое время шары упадут на стол. Применим формулу для трех шаров:

$${h_1} = \frac{{gt_1^2}}{2} \Rightarrow {t_1} = \sqrt {\frac{{2{h_1}}}{g}}$$

$${h_2} = \frac{{gt_2^2}}{2} \Rightarrow {t_2} = \sqrt {\frac{{2{h_2}}}{g}}$$

$${h_3} = \frac{{gt_3^2}}{2} \Rightarrow {t_3} = \sqrt {\frac{{2{h_3}}}{g}}$$

Промежуток времени между ударом первого и второго шара равен:

$${\tau _{12}} = {t_2} — {t_1}$$

$${\tau _{12}} = \sqrt {\frac{{2{h_2}}}{g}}  — \sqrt {\frac{{2{h_1}}}{g}}$$

$${\tau _{12}} = \sqrt {\frac{2}{g}} \left( {\sqrt {{h_2}}  — \sqrt {{h_1}} } \right)$$

Сосчитаем ответ численно:

$${\tau _{12}} = \sqrt {\frac{2}{{10}}} \left( {\sqrt 4  — \sqrt 1 } \right) = 0,447\; с \approx 450\; мс$$

Аналогично найдем время между ударом второго и третьего шара о стол:

$${\tau _{23}} = {t_3} — {t_2}$$

$${\tau _{23}} = \sqrt {\frac{{2{h_3}}}{g}}  — \sqrt {\frac{{2{h_2}}}{g}}$$

$${\tau _{23}} = \sqrt {\frac{2}{g}} \left( {\sqrt {{h_3}}  — \sqrt {{h_2}} } \right)$$

Подсчитаем численно второй промежуток.

$${\tau _{23}} = \sqrt {\frac{2}{{10}}} \left( {\sqrt 9  — \sqrt 4 } \right) = 0,447 \; с \approx 450\; мс$$

Мы видим, что отрезки времени между ударами шаров о стол равны между собой.

Ответ: 450 мс.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.47 Упругий шар, падая с высоты 80 м, после удара о Землю, отскакивает вертикально
1.4.49 Свободно падающее без начальной скорости тело пролетело мимо точки A
1.4.50 За последнюю секунду свободно падающее без начальной скорости тело