Условие задачи:
У паровой турбины радиус рабочего колеса в 8 раз меньше, а число оборотов в единицу времени в 20 раз больше, чем у рабочего колеса гидротурбины. Во сколько раз модуль ускорения точек обода колеса паровой турбины больше, чем у гидротурбины?
Задача №1.8.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_2=\frac{R_1}{8}\), \(\nu_2=20\nu_1\), \(\frac{a_{ц2}}{a_{ц1}}-?\)
Решение задачи:
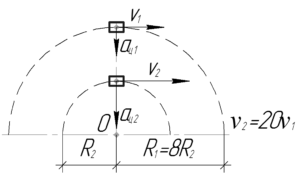 Начнем издалека. Центростремительное ускорение точки на ободе \(a_ц\) можно найти, зная угловую скорость вращения \(\omega\) и радиус колеса \(R\):
Начнем издалека. Центростремительное ускорение точки на ободе \(a_ц\) можно найти, зная угловую скорость вращения \(\omega\) и радиус колеса \(R\):
\[a_ц = {\omega ^2}R\;\;\;\;(1)\]
Поскольку в условии известны только частоты вращения (вернее соотношение частот), то выразим угловую скорость \(\omega\) через частоту \(\nu\).
\[\omega = 2\pi \nu \;\;\;\;(2)\]
Подставим (2) в (1), тогда получим такое выражение:
\[a_ц = {\left( {2\pi \nu } \right)^2}R = 4{\pi ^2}{\nu ^2}R\]
Теперь займемся нахождением ответа на вопроса задачи, для чего распишем отношение ускорений \(\frac{a_{ц2}}{a_{ц1}}\).
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{4{\pi ^2}\nu _2^2{R_2}}}{{4{\pi ^2}\nu _1^2{R_1}}} = \frac{{\nu _2^2{R_2}}}{{\nu _1^2{R_1}}}\]
Так как по условию \(R_2=\frac{R_1}{8}\) и \(\nu_2=20\nu_1\), то:
\[\frac{{{a_{ц2}}}}{{{a_{ц1}}}} = \frac{{400\nu _1^2{R_1}}}{{8\nu _1^2{R_1}}} = \frac{{400}}{8} = 50\]
Ответ: в 50 раз.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.35 Колесо имеет угловую скорость вращения 2pi рад/с. За какое время оно делает
1.1.1 Координата точки меняется со временем по закону x=11+35t+35t^3
1.1.2 Из точек A и B, расположенных на расстоянии 300 м, навстречу друг другу

 icodepro.ru
icodepro.ru
Ты гений
Откуда Взялось значение 400 в последнем действии ?
v_2=20*v_1
Когда возведёте обе части в квадрат, получите 400 в правой части равенства