Условие задачи:
В двух вершинах равностороннего треугольника со стороной 0,5 м находятся точечные заряды 3 и -2 мкКл. Найти потенциал электрического поля в третьей вершине.
Задача №6.3.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=0,5\) м, \(q_1=3\) мкКл, \(q_2=-2\) мкКл, \(\varphi-?\)
Решение задачи:
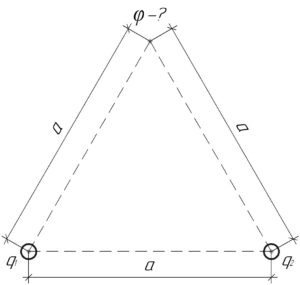 Так как потенциал электрического поля — это скалярная величина, то потенциал электрического поля в третьей вершине \(\varphi\) равен сумме потенциалов полей \(\varphi_1\) и \(\varphi_2\), создаваемых соответственно зарядами \(q_1\) и \(q_2\) в третьей вершине. Поэтому справедлива формула:
Так как потенциал электрического поля — это скалярная величина, то потенциал электрического поля в третьей вершине \(\varphi\) равен сумме потенциалов полей \(\varphi_1\) и \(\varphi_2\), создаваемых соответственно зарядами \(q_1\) и \(q_2\) в третьей вершине. Поэтому справедлива формула:
\[\varphi = {\varphi _1} + {\varphi _2}\;\;\;\;(1)\]
При этом потенциалы \(\varphi_1\) и \(\varphi_2\) можно найти по таким формулам:
\[\left\{ \begin{gathered}
{\varphi _1} = \frac{{k{q_1}}}{a} \hfill \\
{\varphi _2} = \frac{{k{q_2}}}{a} \hfill \\
\end{gathered} \right.\]
Коэффициент пропорциональности \(k\) равен 9·109 Н·м2/Кл2.
Тогда формула (1) примет вид:
\[\varphi = \frac{{k{q_1}}}{a} + \frac{{k{q_2}}}{a}\]
\[\varphi = \frac{k}{a}\left( {{q_1} + {q_2}} \right)\]
Задача решена в общем виде. Посчитаем численное значение потенциала \(\varphi\):
\[\varphi = \frac{{9 \cdot {{10}^9}}}{{0,5}} \cdot \left( {3 \cdot {{10}^{ — 6}} + \left( { — 2 \cdot {{10}^{ — 6}}} \right)} \right) = 18000\;В = 18\;кВ\]
Ответ: 18 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.12 Расстояние между точечными зарядами 10 и -1 нКл равно 1,1 м. Найти
6.3.14 Капля росы в виде шара получилась в результате слияния 216 одинаковых капелек
6.3.15 Электрический пробой воздуха наступает при напряженности поля 3 МВ/м

 icodepro.ru
icodepro.ru