Условие задачи:

В однородном электрическом поле напряженностью 40 кВ/м, направленным горизонтально, находится заряд 27 нКл. Найти напряженность результирующего поля на расстоянии 9 см от заряда в точке, лежащей на прямой, проходящей через заряд и перпендикулярно к силовым линиям.

Задача №6.2.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(E_1=40\) кВ/м, \(q=27\) нКл, \(r=9\) см, \(E-?\)

Решение задачи:

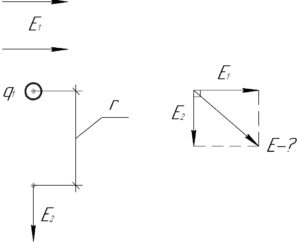В указанной точке модуль напряженности электрического поля \(E_2\), создаваемого зарядом \(q\), легко определить по такой формуле:

\[{E_2} = \frac{{kq}}{{{r^2}}}\;\;\;\;(1)\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

На схеме видно, что напряженности полей \(E_1\) и \(E_2\) перпендикулярны друг другу, поэтому искомую напряженность результирующего поля \(E\) найдём по теореме Пифагора:

\[{E^2} = E_1^2 + E_2^2\]

\[E = \sqrt {E_1^2 + E_2^2} \]

Подставив в последнюю формулу выражение (1), получим решение задачи в общем виде:

\[E = \sqrt {E_1^2 + {{\left( {\frac{{kq}}{{{r^2}}}} \right)}^2}} \]

Произведём вычисления:

\[E = \sqrt {{{\left( {40 \cdot {{10}^3}} \right)}^2} + {{\left( {\frac{{9 \cdot {{10}^9} \cdot 27 \cdot {{10}^{ — 9}}}}{{{{0,09}^2}}}} \right)}^2}} = 50000\;В/м = 500\;В/см \]

Ответ: 500 В/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.21 Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если
6.2.23 Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти
6.2.24 Одинаковые по модулю, но разные по знаку заряды 40 нКл расположены