Условие задачи:
В системах бензин-воздух и стекло-воздух предельные углы полного внутреннего отражения равны соответственно 45° и 30°. Каков предельный угол полного внутреннего отражения для системы стекло-бензин?
Задача №10.4.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha_{пр1}=45^\circ\), \(\alpha_{пр2}=30^\circ\), \(\alpha_{пр3}-?\)
Решение задачи:
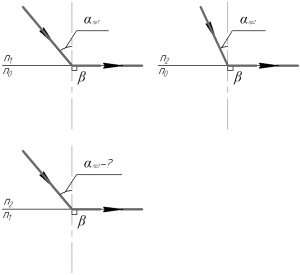 Запишем дважды закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения при переходе светового луча из бензина в воздух и из стекла в воздух (стоит понимать, что явление полного внутреннего отражения наблюдается лишь при переходе из более плотной оптической среды в менее плотную):
Запишем дважды закон преломления света (также известен как закон преломления Снеллиуса) для случая полного внутреннего отражения при переходе светового луча из бензина в воздух и из стекла в воздух (стоит понимать, что явление полного внутреннего отражения наблюдается лишь при переходе из более плотной оптической среды в менее плотную):
\[\left\{ \begin{gathered}
{n_1}\sin {\alpha _{пр1}} = {n_0}\sin \beta \hfill \\
{n_2}\sin {\alpha _{пр2}} = {n_0}\sin \beta \hfill \\
\end{gathered} \right.\]
Здесь \(\alpha_{пр1}\) и \(\alpha_{пр2}\) — соответствующие предельные углы полного внутреннего отражения, \(\beta\) — угол преломления, равный в данном случае 90°, \(n_0\), \(n_1\), \(n_2\) — показатели преломления сред. Показатель преломления воздуха \(n_0\) равен 1. Тогда, так как \(\sin \beta = 1\):
\[\left\{ \begin{gathered}
{n_1}\sin {\alpha _{пр1}} = 1 \hfill \\
{n_2}\sin {\alpha _{пр2}} = 1 \hfill \\
\end{gathered} \right.\]
Имеем:
\[{n_1}\sin {\alpha _{пр1}} = {n_2}\sin {\alpha _{пр2}}\;\;\;\;(1)\]
Тогда:
\[\frac{{{n_1}}}{{{n_2}}} = \frac{{\sin {\alpha _{пр2}}}}{{\sin {\alpha _{пр1}}}}\;\;\;\;(2)\]
Это отношение понадобится нам в дальнейшем решении.
Из равенства (1) видно, что так как \(\alpha_{пр1} > \alpha_{пр2}\), то \({n_1} < {n_2}\), значит явление полного внутреннего отражения будем наблюдаться при переходе света из стекла в бензин. Учитывая это, ещё раз запишем закон преломления Снеллиуса для случая перехода света из стекла в бензин:
\[{n_2}\sin {\alpha _{пр3}} = {n_1}\sin \beta \]
Здесь \(\alpha_{пр3}\) — предельный угол полного внутреннего отражения, \(\beta\) — угол преломления, равный в данном случае 90°, \(n_1\) и \(n_2\) — показатели преломления сред. Тогда, так как \(\sin \beta = 1\):
\[{n_2}\sin {\alpha _{пр3}} = {n_1}\]
\[\sin {\alpha _{пр3}} = \frac{{{n_1}}}{{{n_2}}}\]
\[{\alpha _{пр3}} = \arcsin \left( {\frac{{{n_1}}}{{{n_2}}}} \right)\]
Учитывая равенство (2), окончательно имеем:
\[{\alpha _{пр3}} = \arcsin \left( {\frac{{\sin {\alpha _{пр2}}}}{{\sin {\alpha _{пр1}}}}} \right)\]
Задача решена, подставим данные задачи в полученную формулу и посчитаем численный ответ:
\[{\alpha _{пр3}} = \arcsin \left( {\frac{{\sin 30^\circ }}{{\sin 45^\circ }}} \right) = 45^\circ\]
Ответ: 45°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.4.4 Предельный угол полного внутреннего отражения для льда равен 50°. Определить
10.4.6 В алмазе свет распространяется со скоростью 1,22·10^8 м/с. Определить
10.4.7 Предельный угол полного внутреннего отражения для стекла 45°. Найти скорость

 icodepro.ru
icodepro.ru