Условие задачи:

В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 4 раза больше, чем другого. В широкий сосуд наливают столб воды высотой 102 см. На сколько поднимется ртуть в узком сосуде?

Задача №3.1.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_1=4S_2\), \(h_{в}=102\) см, \(h_2-?\)

Решение задачи:

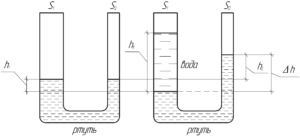На схеме к этой задаче нужно обязательно изобразить начальное состояние, когда в сообщающихся сосудах находится только ртуть, и конечное, когда в широкий сосуд налили воду (смотрите схему).

Изначально свободная поверхность ртути в обоих сосудах находится на одно и том же уровне. Когда в широкий сосуд нальют воду, то уровень ртути в широком сосуде уменьшится на величину \(h_1\), а в узком — увеличится на величину \(h_2\). Эти величины не равны друг другу, так как сечения сосудов не равны. Но так как жидкость несжимаема, значит какой объем ртути «убыл» из широкого сосуда, такой же и «прибыл» в узкий.

\[{S_1}{h_1} = {S_2}{h_2}\]

Так как по условию \(S_1=4S_2\), то:

\[4{S_2}{h_1} = {S_2}{h_2}\]

\[{h_1} = \frac{{{h_2}}}{4}\;\;\;\;(1)\]

Покажем на схеме уровень, ниже которого находится только ртуть. Согласно закону сообщающихся сосудов, при равновесии давление жидкости на горизонтальном уровне одинаково. Поэтому:

\[{\rho _в}g{h_в} = {\rho _{рт}}g\Delta h\]

\[\Delta h = \frac{{{\rho _в}{h_в}}}{{{\rho _{рт}}}}\;\;\;\;(2)\]

Из схемы видно, что:

\[\Delta h = {h_1} + {h_2}\]

Учитывая равенство (1), имеем:

\[\Delta h = \frac{{{h_2}}}{4} + {h_2}\]

\[\Delta h = \frac{{5{h_2}}}{4}\;\;\;\;(3)\]

Приравняем (2) и (3), в итоге получим:

\[\frac{{5{h_2}}}{4} = \frac{{{\rho _в}{h_в}}}{{{\rho _{рт}}}}\]

\[{h_2} = \frac{{4{\rho _в}{h_в}}}{{5{\rho _{рт}}}}\]

Плотность воды \(\rho_{в}=1000\) кг/м³, плотность ртути \(\rho_{рт}=13600\) кг/м³. Переведем высоту столбика воды в систему СИ и посчитаем ответ:

\[102\;см = 1,02\;м\]

\[{h_2} = \frac{{4 \cdot 1000 \cdot 1,02}}{{5 \cdot 13600}} = 0,06\;м = 60\;мм\]

Ответ: 60 мм.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.1.39 В сообщающиеся сосуды налили сначала ртуть. Затем в один сосуд налили масло высотой
3.1.41 Две трубки диаметром 4 см представляют собой сообщающиеся сосуды. В одно колено
3.1.42 Поршень весом 30 Н представляет собой круглый диск радиусом 4 см с отверстием