Условие задачи:

В сосуд налили ртуть и сверху неё масло. Шар в сосуде плавает так, что он ровно наполовину погружен в ртуть, а наполовину — в масло. Определить плотность материала шара.

Задача №3.3.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_{рт}=0,5V\), \(V_{м}=0,5V\), \(\rho-?\)

Решение задачи:

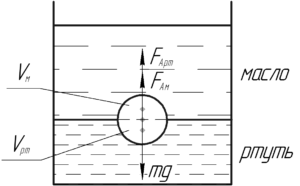На весь шар действует сила тяжести \(mg\). На часть шара, погруженную в ртуть, действует сила Архимеда \(F_{Арт}\). На часть шара, погруженную в масло, действует другая сила Архимеда \(F_{Ам}\). Шар плавает, запишем условие плавания тел:

\[{F_{Арт}} + {F_{Ам}} = mg\]

Распишем силы Архимеда по формуле-определению в левой части, а в правой массу через плотность шара и его полный объем:

\[{\rho _{рт}}g{V_{рт}} + {\rho _м}g{V_{м}} = \rho Vg\]

\[{\rho _{рт}}{V_{рт}} + {\rho _м}{V_{м}} = \rho V\]

Согласно условию шар погружен наполовину в ртуть, а наполовину — в масло (\(V_{рт}=0,5V\), \(V_{м}=0,5V\)), поэтому:

\[0,5{\rho _{рт}}V + 0,5{\rho _м}V = \rho V\]

Таким образом, плотность материала шара \(\rho\) можно найти из такой формулы:

\[\rho  = 0,5\left( {{\rho _{рт}} + {\rho _м}} \right)\]

Плотность ртути \(\rho_{рт}\) равна 13600 кг/м³, а плотность масла \(\rho_{м}\) — 910 кг/м³. Посчитаем ответ:

\[\rho  = 0,5\left( {13600 + 910} \right) = 7255\;кг/м^3 \approx 7,26\;г/см^3\]

Ответ: 7,26 г/см³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.31 Шарик на нити, уравновешенный на весах, опускают в воду. Когда шарик на 0,3 своего
3.3.33 Деревянный шар лежит на дне сосуда с водой, причем половина его находится в воде
3.3.34 На рычажных весах уравновешен сосуд с водой. На сколько нужно увеличить массу гирь