Условие задачи:
В цепь, состоящую из источника ЭДС и сопротивления 2 Ом, включают амперметр сначала последовательно, а затем параллельно сопротивлению. При этом показания амперметра оказываются одинаковыми. Сопротивление амперметра 1 Ом. Определите внутреннее сопротивление источника.
Задача №7.5.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_{сопр}=2\) Ом, \(I_1=I_{22}\), \(R_А=1\) Ом, \(r-?\)
Решение задачи:
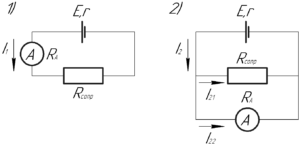 Схемы, для указанных в условии задачи двух случаев, показаны на рисунке. Сначала найдем эквивалентные сопротивления внешней цепи для этих случаев по формулам:
Схемы, для указанных в условии задачи двух случаев, показаны на рисунке. Сначала найдем эквивалентные сопротивления внешней цепи для этих случаев по формулам:
\[\left\{ \begin{gathered}
{R_1} = {R_{сопр}} + {R_А} \hfill \\
{R_2} = \frac{{{R_{сопр}} \cdot {R_А}}}{{{R_{сопр}} + {R_А}}} \hfill \\
\end{gathered} \right.\]
Не будем решать эту задачу в общем виде, поэтому сразу посчитаем значения сопротивлений \(R_1\) и \(R_2\):
\[\left\{ \begin{gathered}
{R_1} = 2 + 1 = 3 \;Ом\hfill \\
{R_2} = \frac{{2 \cdot 1}}{{2 + 1}} = \frac{2}{3} \;Ом\hfill \\
\end{gathered} \right.\]
Также дважды запишем закон Ома для внешней цепи:
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_1} + r}} \hfill \\
{I_2} = \frac{{\rm E}}{{{R_2} + r}} \hfill \\
\end{gathered} \right.\]
Во втором случае сопротивление и амперметр соединены параллельно, а это значит, что они находятся под одинаковым напряжением, поэтому справедливо равенство:
\[{I_{21}}{R_{сопр}} = {I_{22}}{R_А}\]
Откуда ток через сопротивление \(I_{21}\) во втором случае равен:
\[{I_{21}} = {I_{22}}\frac{{{R_А}}}{{{R_{сопр}}}}\]
Учитывая, что \(R_{сопр}=2\) Ом, а \(R_А=1\) Ом, имеем:
\[{I_{21}} =\frac{I_{22}}{2}\;\;\;\;(1)\]
Очевидно, что \(I_2\) равен сумме токов \(I_{21}\) и \(I_{22}\):
\[{I_2} = {I_{21}} + {I_{22}}\]
Принимая во внимание (1), получим:
\[{I_2} = \frac{{3{I_{22}}}}{2} \Rightarrow {I_{22}} = \frac{{2{I_2}}}{3}\]
Имеем:
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_1} + r}} \hfill \\
{I_{22}} = \frac{{2{\rm E}}}{{3\left( {{R_2} + r} \right)}} \hfill \\
\end{gathered} \right.\]
По условию \(I_1=I_{22}\), поэтому:
\[\frac{{\rm E}}{{{R_1} + r}} = \frac{{2{\rm E}}}{{3\left( {{R_2} + r} \right)}}\]
\[\frac{1}{{{R_1} + r}} = \frac{2}{{3\left( {{R_2} + r} \right)}}\]
\[2{R_1} + 2r = 3{R_2} + 3r\]
\[r = 2{R_1} — 3{R_2}\]
Численный ответ к этой задаче равен:
\[r = 2 \cdot 3 — 3 \cdot \frac{2}{3} = 4\;Ом\]
Ответ: 4 Ом.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.28 Два вольтметра, подключенные последовательно к ненагруженной батарее, показывают
7.5.30 Каково удельное сопротивление проводника, если его длина 10 км, площадь поперечного
7.5.31 Медный провод длиной 500 м имеет сопротивление 2,9 Ом. Найти вес провода

 icodepro.ru
icodepro.ru