Условие задачи:

В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами одинаковой жесткости 1500 Н/м. Вначале цилиндр откачан, пружины находятся в ненапряженном состоянии, а поршень — в середине цилиндра. На какое расстояние переместится поршень, если в одну из частей цилиндра ввести 28 г азота при 273 К?

Задача №4.2.102 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$L=2$ м, $k=1500$ Н/м, $m=28$ г, $T=273$ К, $x-?$

Решение задачи:

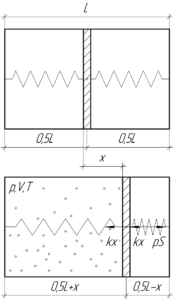Поскольку изначально пружины были не напряжены, то по сути нам необходимо найти деформацию пружин $x$, ведь именно на такую же величину переместится поршень. Обе пружины деформируются на одну и ту же величину, разве что одна растягивается (если в тот объем цилиндра, где находилась эта пружина, был введён азот), а другая — сжимается. Обратите внимание на схеме, куда направлены силы упругости у каждой пружины.

Запишем условие равновесия поршня (первый закон Ньютона) после введения азота (смотрите схему):

$$pS = 2kx\;\;\;\;(1)$$

Азот в конце займёт следующий объем:

$$V = S\left( {\frac{L}{2} + x} \right)\;\;\;\;(2)$$

Применим уравнение Клапейрона-Менделеева для азота:

$$pV = \frac{m}{M}RT$$

Молярная масса азота $M$ равна 0,028 кг/моль.

Учитывая выражение (2), получим:

$$pS\left( {\frac{L}{2} + x} \right) = \frac{m}{M}RT$$

Выразим отсюда произведение $pS$:

$$pS = \frac{{2mRT}}{{M\left( {L + 2x} \right)}}$$

Тогда равенство (1) примет вид:

$$\frac{{2mRT}}{{M\left( {L + 2x} \right)}} = 2kx$$

$$\frac{{mRT}}{{M\left( {L + 2x} \right)}} = kx$$

Запишем это равенство в виде квадратного уравнения относительно $x$:

$$x\left( {L + 2x} \right) = \frac{{mRT}}{{kM}}$$

$$2{x^2} + Lx — \frac{{mRT}}{{kM}} = 0$$

Определим дискриминант:

$$D = {L^2} + \frac{{8mRT}}{{kM}}$$

Тогда искомая величина $x$ равна:

$$x = \frac{{ — L \pm \sqrt {{L^2} + \frac{{8mRT}}{{kM}}} }}{4}$$

Очевидно, что решение, где перед квадратным корнем стоит знак «минус», будет отрицательным, поэтому его можно отбросить.

$$x = \frac{{ — L + \sqrt {{L^2} + \frac{{8mRT}}{{kM}}} }}{4}$$

$$x =  — \frac{L}{4} + \sqrt {\frac{{{L^2}}}{{16}} + \frac{{mRT}}{{2kM}}}$$

Переведём массу в систему СИ и посчитаем ответ:

$$28\;г = 0,028\;кг$$

$$x =  — \frac{2}{4} + \sqrt {\frac{{{2^2}}}{{16}} + \frac{{0,028 \cdot 8,31 \cdot 273}}{{2 \cdot 1500 \cdot 0,028}}}  = 0,5\;м$$

Ответ: 0,5 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.101 В сосуд, на дне которого лежит твердый шар, нагнетают воздух при температуре 27 C
4.2.103 Тонкостенный резиновый шар собственным весом 0,6 Н наполнен неоном и погружен в озеро
4.2.104 Давление воздуха в сосуде равно 102,4 кПа. Вместимость цилиндра разрежающего насоса