Условие задачи:

В замкнутом сосуде к верхней стенке на пружине жесткостью 4 Н/м подвешена сфера объемом 2 л. На какую высоту поднимется сфера, если при постоянной температуре 17° C давление воздуха в сосуде повысить от 100 до 500 кПа?

Задача №4.2.86 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(k=4\) Н/м, \(V=2\) л, \(t=17^\circ\) C, \(p_1=100\) кПа, \(p_2=500\) кПа, \(h-?\)

Решение задачи:

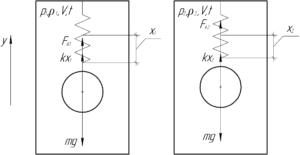На сферу действуют три силы: сила тяжести \(mg\), сила Архимеда \(F_А\) и сила упругости пружины \(kx\).

При разном давлении воздуха в цилиндре плотность воздуха в цилиндре будет разной, а значит разной будет и величина силы Архимеда. Поэтому будет меняться и деформация пружины \(x\).

Неизвестно, была ли пружина изначально растянутой или сжатой. Если она была растянутой, то после увеличения давления она может оставаться растянутой или же сжаться. Также она может быть изначально сжатой, тогда после увеличения давления она сожмётся ещё сильнее. На решение задачи это никак не влияет, мы рассмотрим тот случай, когда пружина всегда растянута. Так как сфера в обоих случаях находится в равновесии, запишем первый закон Ньютона в проекции на ось \(y\) для этих случаев (смотрите схему):

\[\left\{ \begin{gathered}
{F_{А1}} + k{x_1} — mg = 0 \hfill \\
{F_{А2}} + k{x_2} — mg = 0 \hfill \\
\end{gathered} \right.\]

Вычтем из первого равенства второе:

\[{F_{А1}} + k{x_1} — {F_{А2}} — k{x_2} = 0\]

\[k\left( {{x_1} — {x_2}} \right) = {F_{А2}} — {F_{А1}}\]

В этом случае высота подъема сферы определяется по формуле (смотрите схему):

\[h = {x_1} — {x_2}\]

Тогда:

\[kh = {F_{А2}} — {F_{А1}}\;\;\;\;(1)\]

Силу Архимеда \(F_А\) определяют по формуле:

\[{F_А} = \rho Vg\]

Плотность воздуха в сосуде можно найти из уравнения Клапейрона-Менделеева:

\[p = \frac{\rho }{M}RT\]

\[\rho  = \frac{{pM}}{{RT}}\]

Тогда:

\[{F_А} = \frac{{pM}}{{RT}}Vg\]

Формула (1) примет вид:

\[kh = \frac{{{p_2}M}}{{RT}}Vg — \frac{{{p_1}M}}{{RT}}Vg\]

\[kh = \frac{{\left( {{p_2} — {p_1}} \right)M}}{{RT}}Vg\]

\[h = \frac{{\left( {{p_2} — {p_1}} \right)MVg}}{{kRT}}\]

Переведём объем сферы и температуру в цилиндре в систему СИ:

\[2\;л = 0,002\;м^3\]

Посчитаем ответ:

\[h = \frac{{\left( {500 \cdot {{10}^3} — 100 \cdot {{10}^3}} \right) \cdot 0,029 \cdot 0,002 \cdot 10}}{{4 \cdot 8,31 \cdot 290}} = 0,024\;м\]

Ответ: 0,024 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.2.85 На дне цилиндра, наполненного воздухом, плотность которого 1,29 кг/м3, лежит полый
4.2.87 Во сколько раз изменится температура идеального газа, если уменьшить его объем
4.2.88 Внутри закрытого с обоих концов горизонтального цилиндра есть поршень