Условие задачи:

Во сколько раз изменится потенциальная энергия пружины при увеличении её абсолютного удлинения в 3 раза?

Задача №2.8.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(x_2=3x_1\), \(\frac{E_2}{E_1}-?\)

Решение задачи:

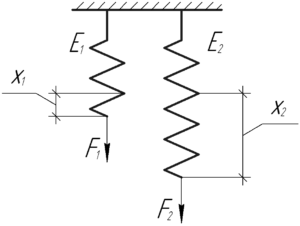Потенциальная энергия пружины определяется её жесткостью \(k\) и величиной абсолютного удлинения \(x\) по такой формуле:

\[E = \frac{{k{x^2}}}{2}\]

Тогда нужное нам отношение распишется таким образом:

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{kx_2^2 \cdot 2}}{{2 \cdot kx_1^2}} = \frac{{x_2^2}}{{x_1^2}}\]

По условию задачи \(x_2=3x_1\), поэтому:

\[\frac{{{E_2}}}{{{E_1}}} = \frac{{{{\left( {3{x_1}} \right)}^2}}}{{x_1^2}} = \frac{{9x_1^2}}{{x_1^2}} = 9\]

Ответ: увеличится в 9 раз.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.10 Винтовка массой 2,8 кг подвешена горизонтально на двух параллельных нитях
2.8.12 Два шарика движутся навстречу друг другу со скоростями 1 и 0,5 м/с. После удара
2.8.13 Камень массой 2 кг брошен вертикально вверх, его начальная кинетическая энергия