Условие задачи:

За первую секунду равноускоренного движения тело проходит путь равный 1 м, а за вторую — 2 м. Какой путь пройдет тело за третью секунду движения?

Задача №1.3.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(S_1=1\) м, \(S_2=2\) м, \(S_3-?\)

Решение задачи:

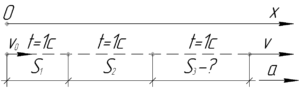Путь за любую n-ую секунду можно найти, отняв из пути за n секунд путь за (n-1) секунд. Этот алгоритм работает и для пути за первую секунду, он будет равен разность пути за одну секунду и пути за 0 секунд, т.е. просто пути за одну секунду.

Примем \(t_1 =1\) с, \(t_2 =2\) с и \(t_3 =3\) с.

Тело двигалось равноускоренно, причем ничего не сказано о его начальной скорости, поэтому будем думать, что она у тела имелась. Запишем уравнение движения:

\[S\left( t \right) = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]

Принимая во внимание наши первые рассуждения, запишем систему уравнений.

\[\left\{ \begin{gathered}
{S_1} = S\left( {{t_1}} \right) \hfill \\
{S_2} = S\left( {{t_2}} \right) — S\left( {{t_1}} \right) \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_1} + \frac{{at_1^2}}{2} \hfill \\
{S_2} = {\upsilon _0}{t_2} + \frac{{at_2^2}}{2} — \left( {{\upsilon _0}{t_1} + \frac{{at_1^2}}{2}} \right) \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_1} + \frac{{at_1^2}}{2} \hfill \\
{S_2} = {\upsilon _0}\left( {{t_2} — {t_1}} \right) + \frac{{a\left( {t_2^2 — t_1^2} \right)}}{2} \hfill \\
\end{gathered} \right.\]

Заменим величины их численными значениями, получим систему из двух уравнений с двумя неизвестными.

\[\left\{ \begin{gathered}
1 = {\upsilon _0} + 0,5a \hfill \\
2 = {\upsilon _0} + 1,5a \hfill \\
\end{gathered} \right.\]

Отнимем из нижнего уравнения верхнее и сразу получим численное значение ускорения \(a\).

\[a = 1\;м/с^2\]

Подставив его в любое из уравнений, легко получим начальную скорость \(\upsilon_0\).

\[1 = {\upsilon _0} + 0,5 \cdot 1\]

\[{\upsilon _0} = 0,5\; м/с\]

Искомый путь за третью секунды найдем из формулы:

\[{S_3} = {\upsilon _0}\left( {{t_3} — {t_2}} \right) + \frac{{a\left( {t_3^2 — t_2^2} \right)}}{2}\]

В итоге:

\[{S_3} = 0,5 \cdot \left( {3 — 2} \right) + \frac{{1 \cdot \left( {{3^2} — {2^2}} \right)}}{2} = 3\; м\]

Ответ: 3 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.43 Два велосипедиста едут навстречу: один из них, имея скорость 7,2 км/ч, спускается
1.3.45 По наклонной доске пустили снизу вверх шарик. На расстоянии 30 см от начала
1.3.46 Тело, двигаясь с начальной скоростью 10 м/с и постоянным ускорением 10 м/с2