icodepro.ruУсловие задачи:
Аэростат поднимается вертикально вверх с ускорением 2 м/с2. Через 5 с от начала движения из него выпал предмет. Через какое время предмет упадет на Землю?
Задача №1.4.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(a=2\) м/с2, \(\tau=5\) с, \(t-?\)
Решение задачи:
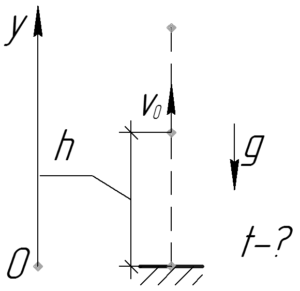Аэростат вместе с предметом начинает движение с поверхности земли. Хотя это и не написано в условии, но подразумевается, что это так.
Через время \(\tau\) они, благодаря ускорению \(a\), достигнут какой-то высоты \(h\). Это ускорение создают какие-то силы, например, сила Архимеда, сила тяжести и т.д, в данном случае они не важны, поскольку это задача на кинематику, а не динамику. Её (высоту) легко определить по следующей формуле:
\[h = \frac{{a{{\tau}^2}}}{2}\;\;\;\;(1)\]
Но если аэростат двигался равноускоренно, значит через \(\tau\) и у аэростата, и у предмета будет какая-то скорость \(\upsilon _0\), которая сохранится у тела и по величине, и по направлению после выпадения из аэростата. Найдем \(\upsilon _0\) таким образом.
\[{\upsilon _0} = a\tau\;\;\;\;(2)\]
Начальная скорость предмета — это и есть скорость аэростата в момент выпадения предмета. Но на его ускорение (после падения) никак не повлияет ускорение аэростата. Ускорение создается только силами, действующими на тело, а они разные для аэростата и предмета.
Если записать уравнение движения предмета, то оно будет выглядеть следующим образом:
\[oy:y = h + {\upsilon _0}t — \frac{{g{t^2}}}{2}\;\;\;\;(3)\]
Знак «плюс» перед слагаемым \({\upsilon _0}t\) показывает, что скорость в момент выпадения камня сонаправлена с осью \(y\), знак «минус» перед \(\frac{{g{t^2}}}{2}\) — то, что ускорение противонаправлено введенной оси.
Когда предмет долетит до земли через время \(t\), то его координата \(y\) станет равна нулю, поэтому приравняем уравнение (3) к нулю:
\[h + {\upsilon _0}t — \frac{{g{t^2}}}{2} = 0\]
Подставим в полученное выражение формулы для \(h\) (см. формулу (1)) и \(\upsilon_0\) (см. формулу (2)):
\[\frac{{a{{\tau}^2}}}{2} + a{\tau}{t} — \frac{{g{t^2}}}{2} = 0\]
Умножим обе части полученного уравнения на (-1):
\[\frac{{g{t^2}}}{2} — a\tau t — \frac{{a{\tau ^2}}}{2} = 0\]
Решим это квадратное уравнение, заменив буквенные обозначения численными данными из условия. Это действие не повлияет на ответ, поскольку все исходные данные даны в системе СИ, поэтому и ответ мы получим в ней же.
\[5t^2 — 10t — 25 = 0\]
\[t^2 — 2t — 5 = 0\]
Определим дискриминант квадратного уравнения \(D\).
\[D = 4 + 4 \cdot 5 = 24\]
\[t = \frac{{2 \pm \sqrt {24} }}{2} = 1 \pm \sqrt 6 \]
\[\left[ \begin{gathered}
t = 3,45 \; с \hfill \\
t = — 1,45 \; с \hfill \\
\end{gathered} \right.\]
Отбрасываем отрицательный корень и получаем ответ к задаче.
Ответ: 3,45 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.31 Человек, стоящий на краю высохшего колодца, бросает вертикально вверх
1.4.33 С аэростата, опускающегося со скоростью 5 м/с, бросают вертикально вверх тело
1.4.34 С вертолета, находящегося на высоте 300 м, сброшен груз. Через какое время
Скажите ,а почему у предмета здесь есть начальная скорость? Он же падает без неё в задаче сказано.
Скорость — это относительная величина. Поэтому начальная скорость предмета зависит от того, какую систему отсчета Вы выбрали. Если рассматривать относительно аэростата, то скорость предмета действительно равна нулю. А вот если относительно Земли (что я делал в решении), то его скорость равна скорости аэростата в момент выпадения предмета.
Чтобы объяснить это, приведу аналогию. Вы подбираете на улице камень и садитесь в автобус. Автобус начинает ехать с ускорением \(a\), через любое произвольное время \(t\) его скорость относительно Земли будет равна \(\upsilon=at\). Если Вы неподвижно сидите в автобусе, то Ваша скорость (и скорость камня в Вашем кармане) относительно Земли также будет равна \(\upsilon=at\). Если Вы движетесь вместе с автобусом (точнее — Вы неподвижны относительно автобуса), то в любой момент времени Ваша скорость и скорость камня относительно Земли равна скорости автобуса относительно Земли.
Далее Вы высовываете руку с камнем в форточку и просто его отпускаете. В момент отпускания его скорость относительно Земли также будет равна \(\upsilon=at\) (а относительно автобуса — нулю).
Интересно: Вы (в автобусе) будете наблюдать, как камень падает ускоренно (с ускорением равным \(g\)) вертикально вниз по прямой. А наблюдатель на улице будет видеть, что камень падает ускоренно (с ускорением равным \(g\)) с горизонтальной начальной скоростью \(\upsilon=at\) по ветви параболы.
Помогите пожалуйста решить Лодка массой 80 кг отплывает от берега со скоростью ?1, направленнойпод углом 30° к линии берега. С берега на лодку с разгона прыгает юношамассой 40 кг со скоростью 6 м/с, перпендикулярной линии берега. При этомлодка продолжает движение под углом 60° к линии берега. Первоначальнаяскорость лодки равна:
уровнение движения нужно всегда использовать?
Не всегда, это зависит от задачи
Почему -10t? a*тау = +10?
Обе части полученного мною квадратного уравнения
\[\frac{{a{{\tau}^2}}}{2} + a{\tau}{t} — \frac{{g{t^2}}}{2} = 0\]
я умножил на (-1). Я об этом умолчал в решении (полагал, что это итак понятно), но теперь добавил эту информацию.
А зачем записывать уравнение движения предмета,если оно никак не помогло. И что за переменная t?
Ещё как помогло, мы потом приравниваем его к нулю и оттуда находим искомое время \(t\) (ранее было \(t_1\)). Время \(\tau\) (ранее было \(t\)) — это время движения аэростата вверх до выпадения предмета, оно известно из условия.
Я поменял обозначение переменных, добавил пояснения, думаю сейчас станет понятнее.
Спаааасибо огромное, понятно обьяснили, дошло))))
Знак «плюс» перед слагаемым ?0t показывает, что скорость в момент выпадения камня сонаправлена с осью y, знак «минус» перед gt22 — то, что ускорение противонаправлено введенной оси. Только не понял этой строчки. Наоборот же, ось Y идет вверх, значит камень, падая, в
летит вниз, против оси Y, а ускорение направлено вверх, по оси Y. Обьясните пожалуйста, что я не так пониимаю?
После выпадения камня из аэростата он движется с ускорением \(g\), которое направлено вниз, против оси \(y\).
Спасибо огромное , очень помогли
А как мы получили, что начальная скорость тела равна at?
Потому что аэростат и тело (до его выпадения) движутся вместе, поэтому их скорости равны. Вы же согласны с тем, что скорость аэростата (а значит и тела) через время t, зная его ускорение a, можно найти по формуле at?
А можно было рассматривать движение после выпадения тела из аэростата до потери начальной скорости и его свободное падение? Я на олимпиаде получил тот же ответ, кроме отрицательного.
Не совсем понятно зачем это движение делить на два, «до потери начальной скорости и его свободное падение». А до потери начальной скорости — это разве не свободное падение?
У проверяющих олимпиады есть критерии оценки, думаю они достойно и правильно оценят ваше решение.
oy:y=h+?0t—gt22 Откуда это формула?
Я записал уравнение движения тела вдоль оси y, которое в общем виде выглядит так:
y=y0+v0t+gt^2/2
Здесь:
1) y0 — начальная координата, в нашем случае равная h;
2) v0 — начальная скорость, имеет знак «+», поскольку вектор скорости сонаправлен с осью y;
3) перед gt^2/2 стоит знак «-«, так как ускорение свободного падения направлено в другую сторону, нежели ось y.
5t1^2—10t1—25=0
t1^2—2t1—5=0 это как получилось
куда а и g исчезли
«Решим это квадратное уравнение, заменив буквенные обозначения численными данными из условия.» Я просто подставил значения этих величин.
Поделил на 5 каждый член
А откуда «D=4+4x5?
Чтобы решить квадратное уравнение, нужно найти дискриминант D.
Для квадратного уравнения вида ax^2+bx+c=0 дискриминант вычисляют по такой формуле:
D=b^2-4ac
Вот, что, значит объяснили!!! Благодарность огрооомная!!!
Не за что!