Условие задачи:
Аккумулятор замкнут на некоторый проводник. Если в цепь включить два амперметра, соединенные между собой параллельно, то они покажут силу тока 2 и 3 А. Если амперметры включить в цепь последовательно, то они покажут 4 А. Каким будет ток в цепи в отсутствие амперметров?
Задача №7.5.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(I_{11}=2\) А, \(I_{12}=3\) А, \(I_2=4\) А, \(I_3-?\)
Решение задачи:
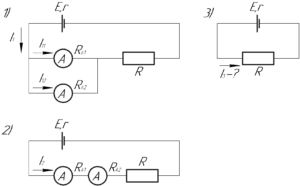 В задаче рассмотрено три случая, схемы для которых приведены на рисунке. Очевидно, что в первом случае общий ток в цепи равен сумме токов \(I_{11}\) и \(I_{12}\), то есть:
В задаче рассмотрено три случая, схемы для которых приведены на рисунке. Очевидно, что в первом случае общий ток в цепи равен сумме токов \(I_{11}\) и \(I_{12}\), то есть:
\[{I_1} = {I_{11}} + {I_{12}}\]
\[{I_1} = 2 + 3 = 5\;А\]
Также должно быть понятно, что внутренние сопротивления амперметров \(R_{А1}\) и \(R_{А2}\) различны, поскольку в противном случае токи \(I_{11}\) и \(I_{12}\) были бы равны. В первом случае амперметры, соединенные параллельно, находятся под одинаковым напряжением, поэтому верно равенство:
\[{I_{11}}{R_{А1}} = {I_{12}}{R_{А2}}\]
Откуда имеем:
\[{R_{А1}} = {R_{А2}}\frac{{{I_{12}}}}{{{I_{11}}}}\]
Учитывая, что \(I_{11}=2\) А, а \(I_{12}=3\) А, получим:
\[{R_{А1}} = 1,5{R_{А2}}\]
Тогда в первом случае суммарное сопротивление двух амперметров равно \(2,5R_{А2}\), а во втором — \(0,6R_{А2}\) (чтобы убедиться в этом, воспользуйтесь формулами нахождения сопротивления последовательно и параллельно соединенных проводников).
Запишем закон Ома для полной цепи для всех трех случаев:
\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{0,6{R_{А2}} + R + r}} \;\;\;\;(1)\hfill \\
{I_2} = \frac{{\rm E}}{{2,5{R_{А2}} + R + r}} \;\;\;\;(2)\hfill \\
{I_3} = \frac{{\rm E}}{{R + r}} \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]
Разделим (1) на (2):
\[\frac{{{I_1}}}{{{I_2}}} = \frac{{2,5{R_{А2}} + R + r}}{{0,6{R_{А2}} + R + r}}\]
Учтем, что \(I_1=5\) А, а \(I_2=4\) А:
\[\frac{5}{4} = \frac{{2,5{R_{А2}} + R + r}}{{0,6{R_{А2}} + R + r}}\]
Перемножим «крест-накрест»:
\[3{R_{А2}} + 5\left( {R + r} \right) = 10{R_{А2}} + 4\left( {R + r} \right)\]
\[7{R_{А2}} = R + r\]
\[{R_{А2}} = \frac{{R + r}}{7}\]
Полученное выражение подставим в (1):
\[{I_1} = \frac{{\rm E}}{{\frac{6}{{10}}\left( {\frac{{R + r}}{7}} \right) + R + r}}\]
\[{I_1} = \frac{{\rm E}}{{\frac{{76}}{{70}}\left( {R + r} \right)}}\]
\[{I_1} = \frac{{70{\rm E}}}{{76\left( {R + r} \right)}}\]
Если принять во внимание (3), получим:
\[{I_1} = \frac{{70{I_3}}}{{76}}\]
\[{I_1} = \frac{{35{I_3}}}{{38}}\]
Окончательно получим:
\[{I_3} = \frac{{38{I_1}}}{{35}}\]
\[{I_3} = \frac{{38 \cdot 5}}{{35}} = 5,43\;А\]
Ответ: 5,43 А.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.25 Вольтметр, подключенный к источнику с ЭДС 12 В, показывает напряжение 9 В. К его клеммам
7.5.27 К источнику тока подключены последовательно амперметр и резистор. Параллельно резистору
7.5.28 Два вольтметра, подключенные последовательно к ненагруженной батарее, показывают

 icodepro.ru
icodepro.ru
Подскажите пожалуйста, для чего мы добавляем сопротивление?
Исходя из условия задачи должно быть понятно, что у амперметров в этой задаче должны быть сопротивления. Если бы их не было, что в первом случае через амперметры шел одинаковый ток, а во втором — ток должен был быть равен суммарному току через амперметры в первом случае.
Вообще говоря, сопротивление у электроизмерительных приборов есть всегда. У амперметров его стараются сделать очень маленьким, а у вольтметров — очень большим.