Условие задачи:

Автомобиль двигался со скоростью 4 м/с, затем был выключен двигатель и началось торможение с ускорением 1 м/с². Какой путь пройден автомобилем за 5 с с момента начала торможения?

Задача №1.3.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_0=4\) м/с, \(a=1\) м/с², \(t=5\) с, \(S-?\)

Решение задачи:

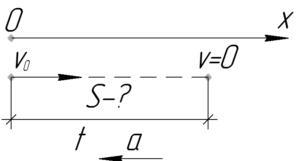Вам может показаться, что задача решается в одну строку, просто записав уравнение движения и вычислив ответ. Но не тут-то было! Зная начальную скорость \(\upsilon_0\) и ускорение \(a\), найдем время движения автомобиля до остановки, для чего запишем формулу скорости для равнозамедленного движения.

\[\upsilon  = {\upsilon _0} — at\]

Когда машина остановится, ее скорость \(\upsilon\) будет равна нулю. Решим получившееся линейное уравнение.

\[\upsilon  = 0 \Rightarrow {\upsilon _0} — at = 0 \Rightarrow t = \frac{{{\upsilon _0}}}{a}\]

Любопытства ради сосчитаем численное значение этого времени.

\[t = \frac{4}{1} = 4\; с \]

Получатся, что тело двигалось четыре секунды, а не пять, и если бы мы решали задачу в лоб (как написано в первом абзаце), то непременно бы ошиблись. Запишем уравнение движения нашего авто и подставим в него полученное выражение для времени.

\[S = {\upsilon _0}t — \frac{{a{t^2}}}{2}\]

\[S = {\upsilon _0}\frac{{{\upsilon _0}}}{a} — \frac{a}{2}{\left( {\frac{{{\upsilon _0}}}{a}} \right)^2} = \frac{{\upsilon _0^2}}{{2a}}\]

Интересно, но этот же ответ можно получить из такой известной формулы:

\[{\upsilon ^2} — \upsilon _0^2 =  — 2aS\]

Конечная скорость \(\upsilon\) отсутствует, поэтому справедливо:

\[\upsilon _0^2 = 2aS \Rightarrow S = \frac{{\upsilon _0^2}}{{2a}}\]

Если в условии задачи дано какое-то время, то обычно все напрочь забывают эту формулу. Но, как Вы сами видите, задача таким способом решается короче, быстрее, а, самое главное, верно!

Так какой же ответ в задаче? Давайте его сосчитаем.

\[S = \frac{{{4^2}}}{{2 \cdot 1}} = 8\; м \]

Ответ: 8 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.27 У светофора трактор, движущийся равномерно со скоростью 18 км/ч, обогнал
1.3.29 Автомобиль начал двигаться с ускорением 1,5 м/с2 и через некоторое время
1.3.30 Автомобиль, двигаясь равноускоренно, прошел два смежных участка пути