Решение: Автомобиль, двигаясь равномерно со скоростью 45 км/ч, в течение 10 с прошел

Условие задачи:

Автомобиль, двигаясь равномерно со скоростью 45 км/ч, в течение 10 с прошел путь такой же, как автобус, двигавшийся в том же направлении с постоянной скоростью, за время 15 с. Какова скорость автомобиля относительно скорости автобуса?

Задача №1.7.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_1=45\) км/ч, \(t_1=10\) с, \(S_1=S_2\), \(t_2=15\) с, \(\upsilon_{12}-?\)

Решение задачи:

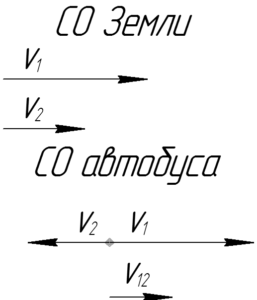Так как сказано, что автомобиль и автобус прошли одно и то же расстояние (\(S_1=S_2\)), то легко найти скорость автобуса относительно Земли.

\[{S_1} = {S_2}\]

\[{\upsilon _1}{t_1} = {\upsilon _2}{t_2} \Rightarrow {\upsilon _2} = {\upsilon _1}\frac{{{t_1}}}{{{t_2}}}\]

Чтобы найти вектор скорости автомобиля относительно автобуса \(\overrightarrow {{\upsilon _{12}}}\), необходимо к вектору скорости автомобиля \(\overrightarrow {{\upsilon _1}}\) прибавить вектор, равный по величине и противоположный по направлению вектору скорости автобуса \(— \overrightarrow {{\upsilon _2}}\). Все это наглядно продемонстрировано на рисунке справа.

Модуль вектора \(\upsilon_{12}\) равен, так как \(\upsilon_{1}>\upsilon_{2}\):

\[{\upsilon _{12}} = {\upsilon _1} — {\upsilon _2}\]

Подставим полученное ранее выражение:

\[{\upsilon _{12}} = {\upsilon _1} — {\upsilon _1}\frac{{{t_1}}}{{{t_2}}} = {\upsilon _1}\left( {1 — \frac{{{t_1}}}{{{t_2}}}} \right)\]

\[45\; км/ч = \frac{{45 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{450}}{{36}}\; м/с = 12,5\; м/с \]

В итоге:

\[{\upsilon _{12}} = 12,5\left( {1 — \frac{{10}}{{15}}} \right) = 4,17\; м/с\]