Условие задачи:
Автомобиль движется со скоростью 12 м/с. Чему равен модуль линейной скорости верхней точки протектора колеса автомобиля относительно земли?
Задача №1.7.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon=12\) м/с, \(\upsilon_в-?\)
Решение задачи:
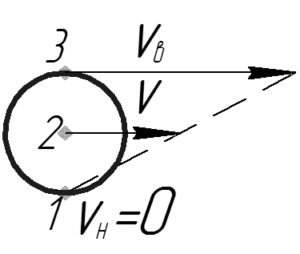 Колесо совершает плоскопараллельное движение: она одновременно вращается вокруг своей оси и движется поступательно. При этом скорость любой точки — это векторная сумма вращательной и поступательной скоростей точки.
Колесо совершает плоскопараллельное движение: она одновременно вращается вокруг своей оси и движется поступательно. При этом скорость любой точки — это векторная сумма вращательной и поступательной скоростей точки.
При таком движении всегда существует точка, скорость которого в данный момент времени равна нулю. Если колесо не проскальзывает, то такой точкой является точка касания колеса с дорогой (точка 1 на рисунке). Эту точку также называют мгновенный центром скоростей (МЦС).
Интересно, что в этот момент времени все точки колеса совершают вращательное движение (естественно с одной угловой скоростью) вокруг МЦС. Поэтому верно записать следующее:
\[\left\{ \begin{gathered}
\upsilon = \omega \cdot R \hfill \\
{\upsilon _в} = \omega \cdot 2R \hfill \\
\end{gathered} \right.\]
\(R\) — это радиус колеса.
Тогда очевидно, что:
\[{\upsilon _в} = 2\upsilon \]
\[{\upsilon _в} = 2 \cdot 12 = 24\; м/с\]
Ответ: 24 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.23 Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после
1.7.25 Человек бежит со скоростью 5 м/с относительно палубы теплохода в направлении
1.7.26 При движении моторной лодки по течению реки ее скорость относительно берега

 icodepro.ru
icodepro.ru
Почему скорость в нижней точке колеса, обозначенной цифрой 1 будет равна нулю?
Потому что колесо совершает сложное движение: оно состоит из поступательного и вращательного движений. При этом скорость каждой точки есть векторная сумма скоростей вращательного и поступательного движений. Если предположить, что проскальзывание отсутствует, то такая векторная сумма скоростей для точки 1 будет как раз равна нулю.
С колесом этот факт не очень нагляден. Но представьте себе трактор на гусеничном ходу — полагаю, вы согласитесь, что нижние траки (или как там они называются) абсолютно неподвижны относительно земли.