Решение: Батарея элементов замкнута двумя проводниками сопротивлением 4 Ом каждый

Условие задачи:

Батарея элементов замкнута двумя проводниками сопротивлением 4 Ом каждый, соединенный параллельно. При этом напряжение на зажимах батареи 6 В. Если один проводник отключить, напряжение на зажимах будет 8 В. Определите ЭДС и внутреннее сопротивление батареи.

Задача №7.2.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=4\) Ом, \(U_1=6\) В, \(U_2=8\) В, \(\rm E-?\), \(r-?\)

Решение задачи:

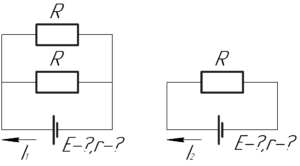Если в первом случае через батарею течет ток \(I_1\), а внешнее сопротивление цепи равно \(R_1\), то напряжение на зажимах батареи \(U_1\) в этом случае равно:

\[{U_1} = {I_1}{R_1}\]

Аналогично, во втором случае напряжение на зажимах батареи \(U_2\) равно:

\[{U_2} = {I_2}{R_2}\]

То есть мы имеем такую систему:

\[\left\{ \begin{gathered}
{U_1} = {I_1}{R_1} \hfill \\
{U_2} = {I_2}{R_2} \hfill \\
\end{gathered} \right.\]

Очевидно, что внешнее сопротивление цепи \(R_1\) в первом случае равно эквивалентному сопротивлению двух одинаковых параллельно соединенных проводников \(R\), а во втором — сопротивлению проводника \(R\), то есть:

\[\left\{ \begin{gathered}
{R_1} = \frac{R}{2} \hfill \\
{R_2} = R \hfill \\
\end{gathered} \right.\]

Силы тока \(I_1\) и \(I_2\) определим, воспользовавшись законом Ома для полной цепи:

\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_1} + r}} \hfill \\
{I_2} = \frac{{\rm E}}{{{R_2} + r}} \hfill \\
\end{gathered} \right.\]

Учитывая ранее полученные выражения для сопротивлений, имеем:

\[\left\{ \begin{gathered}
{I_1} = \frac{{2{\rm E}}}{{R + 2r}} \hfill \\
{I_2} = \frac{{\rm E}}{{R + r}} \hfill \\
\end{gathered} \right.\]

Тогда самая первая система привет вид:

\[\left\{ \begin{gathered}
{U_1} = \frac{{{\rm E}R}}{{R + 2r}} \hfill \\
{U_2} = \frac{{{\rm E}R}}{{R + r}} \;\;\;\;(1)\hfill \\
\end{gathered} \right.\]

Значит мы имеем такое равенство:

\[{U_1}\left( {R + 2r} \right) = {U_2}\left( {R + r} \right)\]

Раскроем скобки в обеих частях равенства, все члены с неизвестным \(r\) перенесем в левую часть, остальные — в правую, далее вынесем неизвестное внутреннее сопротивление \(r\) за скобки и выразим его:

\[{U_1}R + 2{U_1}r = {U_2}R + {U_2}r\]

\[2{U_1}r — {U_2}r = {U_2}R — {U_1}R\]

\[r\left( {2{U_1} — {U_2}} \right) = R\left( {{U_2} — {U_1}} \right)\]

\[r = \frac{{R\left( {{U_2} — {U_1}} \right)}}{{2{U_1} — {U_2}}}\;\;\;\;(2)\]

Отлично, на один вопрос задачи мы ответили. Давайте из формулы (1) выразим ЭДС:

\[{\rm E} = {U_2}\frac{{R + r}}{R}\]

\[{\rm E} = {U_2}\left( {1 + \frac{r}{R}} \right)\]

Подставим в эту формулу выражение (2):

\[{\rm E} = {U_2}\left( {1 + \frac{{{U_2} — {U_1}}}{{2{U_1} — {U_2}}}} \right)\]

В скобках приведем под общий знаменатель:

\[{\rm E} = {U_2}\frac{{2{U_1} — {U_2} + {U_2} — {U_1}}}{{2{U_1} — {U_2}}}\]

\[{\rm E} = \frac{{{U_1}{U_2}}}{{2{U_1} — {U_2}}}\]