Условие задачи:
Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с, равна высоте, с которой его бросили. Чему равна эта высота?
Задача №1.5.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=4,9\) м/с, \(L=H\), \(H-?\)
Решение задачи:
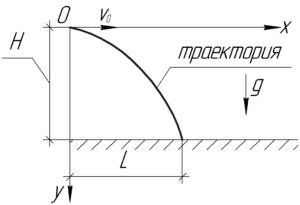 Сделав простой рисунок, запишем уравнения движения тела в проекциях на оси \(x\) и \(y\).
Сделав простой рисунок, запишем уравнения движения тела в проекциях на оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:x = {\upsilon _0}t\,\,\,\,\,\, \hfill \\
oy:y = \frac{{g{t^2}}}{2}\,\,\, \hfill \\
\end{gathered} \right.\]
Естественно, если принять \(t\) за время полета тела, то справедливо:
\[\left\{ \begin{gathered}
L = {\upsilon _0}t\,\,\,\,\,\,(1) \hfill \\
H = \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Здесь \(L\) — дальность полета тела по горизонтали, \(H\) — высота, с которой оно упало.
Так как по условию задачи дальность полета тела равна высоте \(L=H\), с которой его сбросили, то приравняем формулы (1) и (2) для того, чтобы найти время \(t\).
\[L = H \Rightarrow {\upsilon _0}t = \frac{{g{t^2}}}{2} \Rightarrow t = \frac{{2{\upsilon _0}}}{g}\]
Подставим в формулу (2) найденное выражение:
\[H = \frac{g}{2}{\left( {\frac{{2{\upsilon _0}}}{g}} \right)^2} = \frac{{2\upsilon _0^2}}{g}\]
Сосчитаем ответ, подставив данные нам численные данные:
\[H = \frac{{2 \cdot {{4,9}^2}}}{{9,8}} = 4,9\; м \]
Ответ: 4,9 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.5.3 В горизонтальном направлении со скоростью 10 м/с брошено тело, которое
1.5.5 Два тела брошены с высоты 100 м, первое — с горизонтальной скоростью 5 м
1.5.6 Камень, брошенный горизонтально с вышки, через 3 с упал на землю

 icodepro.ru
icodepro.ru
разве в предпоследнем действии 2 не должно быть в квадрате и превратиться в 4?
вопрос исчерпан
хахххаха
нам учитель дал формулу h=v0t + gt^2\2, а здесь она h=gt^2\2, кому верить?
Верить всё-таки нам — первая ваша формула работает только для движения тела, брошенного вертикального вниз с начальной скоростью. У нас же тело бросают горизонтально.
Почему во всех заданиях мы берем g=10, а тут 9,8?
Это некритично, можете брать хоть 10, хоть 9,8.
Я взял 9,8, чтобы мой ответ совпал с ответом в сборнике.