Условие задачи:
Дифракционная линия для волны 546,1 нм в спектре первого порядка наблюдается под углом 19°. Определить наибольший порядок спектра, который может образовать эта дифракционная решетка.
Задача №10.7.18 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\lambda=546,1\) нм, \(k_1=1\), \(\varphi_1=19^\circ\), \(k_{\max}-?\)
Решение задачи:
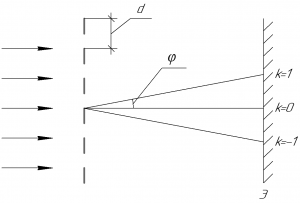 Запишем формулу дифракционной решетки:
Запишем формулу дифракционной решетки:
\[d\sin \varphi = k\lambda\;\;\;\;(1)\]
В этой формуле \(d\) — период решетки (также называют постоянной решетки), \(\varphi\) — угол дифракции, \(k\) — порядок максимума, \(\lambda\) — длина волны, падающей нормально на решетку.
Благодаря тому, что нам известны все параметры первого дифракционного максимума, из формулы (1) мы можем определить неизвестный период решетки:
\[d = \frac{{{k_1}\lambda }}{{\sin {\varphi _1}}}\;\;\;\;(2)\]
Для нахождения максимального порядка дифракционного спектра необходимо воспользоваться следующими соображениями. Угол дифракции не может быть больше 90°, поэтому нужно определить порядок дифракционного максимума для \(\varphi=90^\circ\), то есть \(\sin \varphi = 1\). Для нахождения наибольшего порядка дифракционного спектра, нужно взять целую часть полученного числа. Ни в коем случае не округляйте в большую сторону! В таком случае при подстановке вашего наибольшего порядка в формулу дифракции Вы будете получать синус больше 1, чего быть не должно!
Итак, если \(\sin \varphi = 1\), то:
\[d = k\lambda \]
Откуда:
\[k = \frac{d}{\lambda }\]
Учитывая (2), имеем:
\[k = \frac{{{k_1}\lambda }}{{\sin {\varphi _1} \cdot \lambda }}\]
\[k = \frac{{{k_1}}}{{\sin {\varphi _1}}}\]
Подставим численные данные задачи в эту формулу:
\[k = \frac{1}{{\sin 19^\circ }} = 3,07\]
Взяв целую часть числа, получим \(k_{\max}=3\).
Ответ: 3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.7.17 Найти наибольший порядок спектра для света с длиной волны 700 нм, если постоянная
10.7.19 Сколько максимумов можно будет увидеть на экране, если на дифракционную решетку
10.7.20 Постоянная дифракционной решетки в 3,7 раза больше длины световой волны, нормально

 icodepro.ru
icodepro.ru