Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой

Условие задачи:

Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой наименьшей скорости автомобиль не будет оказывать давления на мост в верхней его точке?

Задача №2.4.2 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R=60\) м, \(P=0\), \(\upsilon-?\)

Решение задачи:

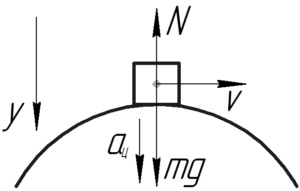Запишем второй закон Ньютона в проекции на ось \(y\), когда автомобиль будет находиться в высшей точке моста.

\[mg – N = m{a_ц}\;\;\;\;(1)\]

Центростремительное ускорение определяют по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(2)\]

Если автомобиль не оказывает давления на мост в верхней точке, значит в этой точке сила реакции опоры \(N\), действующая на автомобиль, равна нулю по третьему закону Ньютона.

\[N = 0\;\;\;\;(3)\]

Учитывая выражения (2) и (3), равенство (1) примет вид:

\[mg = m\frac{{{\upsilon ^2}}}{R}\]

Отсюда выразим искомую скорость \(\upsilon\):

\[\upsilon  = \sqrt {gR} \]

Посчитаем численный ответ к задаче, подставив численные величины в формулу:

\[\upsilon  = \sqrt {10 \cdot 60}  = 24,5\; м/с = 88,2\; км/ч\]

Ответ: 88,2 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.1 Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной