icodepro.ruУсловие задачи:
Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с по выпуклому мосту радиусом 100 м. Определить силу давления автомобиля на мост.
Задача №2.4.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=5\) т, \(\upsilon=10\) м/с, \(R=100\) м, \(P-?\)
Решение задачи:
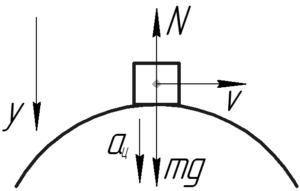Искомая сила давления автомобиля на мост \(P\) равна силе реакции опоры \(N\) согласно третьему закону Ньютона:
\[P = N\;\;\;\;(1)\]
Запишем второй закон Ньютона в проекции на ось \(y\), когда автомобиль будет проезжать по середине моста:
\[mg – N = m{a_ц}\;\;\;\;(2)\]
Центростремительное ускорение найдем по известной формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]
Учитывая формулы (1) и (3), равенство (2) примет вид:
\[mg – P = m\frac{{{\upsilon ^2}}}{R}\]
Выразим силу давления \(P\):
\[P = m\left( {g – \frac{{{\upsilon ^2}}}{R}} \right)\]
Переведем массу автомобиля в систему СИ:
\[5\; т = 5000\; кг\]
Теперь посчитаем численный ответ:
\[P = 5000 \cdot \left( {10 – \frac{{{{10}^2}}}{{100}}} \right) = 45 \cdot {10^3}\; Н = 45\; кН\]
Ответ: 45 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.4 Гирька массой 0,05 кг, привязанная к нити длиной 0,26 м, описывает в горизонтальной
2.4.5 Гиря массой 100 г равномерно вращается на нити в вертикальной плоскости
Извините, можете объяснить когда писать
mg-N=ma а когда наоборот N-mg=ma?
А что тут сложного то
Сначала показываешь все силы, которые действуют на тело. В данном случае на автомобиль действуют такие силы:
– сила тяжести – она направлена к центру Земли;
– сила нормальной реакции опоры – она направлена перпендикулярно опоре.
Далее показываешь, куда направлено ускорение – при движении по окружности оно направлено к центру окружности, в нашем случае – вниз (так как мост выпуклый).
В векторной форме второй закон Ньютона будет выглядеть так:\[m\overrightarrow g + \overrightarrow N = m\overrightarrow a \]Введем какую-нибудь ось (я ввел ось \(y\)), чтобы записать это уравнение в проекции (если вектор направлен так же, как и ось \(y\), то перед модулем вектора ставится “плюс”, иначе – “минус”). Сила тяжести и ускорение у нас сонаправлены с осью, поэтому перед ними знак “плюс”, а вот перед силой нормальной реакции будет “минус”. В итоге получишь:\[mg – N = ma\]
Почему
mg-P=maц
Об этом прекрасно сказано в решении. Из второго закона Ньютона мы имеем:\[mg – N = m{a_ц}\]А из третьего закона Ньютона (тела взаимодействуют с силами, равными по величине, но противоположными по направлению):\[P = N\]Так и получается, что:\[mg – P = m{a_ц}\]
В почему когда мы делаем действие где уже вычисляет P во втором действии с P получилось 45 * на 10 в 3 степени?
И почему потом H=45kH
45000 Н = 45·103 Н = 45 кН
1. Сила давления автомобиля на мост – это вес автомобиля?
2. В разных точках моста вес у автомобиля разный. Почему мы вычисляем его именно в середине моста? Мне кажется, что либо в условии надо спросить вес автомобиля именно в этой точке, либо попросить найти минимальный вес автомобиля.
1. В данном случае да.
2. Я не составляю условия размещённых на сайте задач. Если в условии не сказано в какой точке определить давление автомобиля на мост, значит решающий должен сам выбрать наиболее интересную точку.
Более того, если бы интересующая автора точка была отлична от точки середины моста, то были бы даны привязки (угол с вертикалью, например).
Здравствуйте, у вас в условие написано 5т, а переводе в кг вы ошиблись и написали вместо тонн килограммы
Здравствуйте! Поправил, спасибо за замечание! Вы помогаете нам сделать сайт лучше!