icodepro.ruУсловие задачи:
Бусинка может скользить вдоль гладкого кольца радиуса \(R\), расположенного в вертикальной плоскости. Кольцо вращается вокруг вертикальной оси, проходящей через его центр. Чему равна угловая скорость вращения кольца, при которой бусинка занимает равновесное положение на высоте \(h\) от нижней точки кольца?
Задача №2.4.40 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R\), \(h\), \(\omega-?\)
Решение задачи:
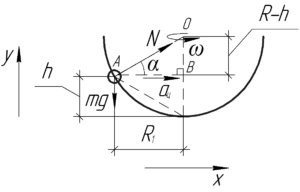На бусинку действуют следующие силы: сила тяжести \(mg\), направленная вертикально, и сила реакции \(N\), направленная от точки касания вдоль радиуса кольца. Вдоль оси \(y\) тело покоится, а в горизонтальной плоскости движется по окружности некоторого радиуса \(R_1\). Записав первый закон Ньютона в проекции на ось \(y\) и второй закон Ньютона в проекции на ось \(x\), получим следующую систему:
\[\left\{ \begin{gathered}
N \cdot \sin \alpha = mg \hfill \\
N \cdot \cos \alpha = m{a_ц} \hfill \\
\end{gathered} \right.\]
Запишем формулу определения ускорения \(a_ц\) через угловую скорость \(\omega\):
\[{a_ц} = {\omega ^2}{R_1}\]
В таком случае система примет следующий вид:
\[\left\{ \begin{gathered}
N \cdot \sin \alpha = mg \hfill \\
N \cdot \cos \alpha = m{\omega ^2}{R_1} \hfill \\
\end{gathered} \right.\]
Верхнее равенство системы поделим на нижнее, тогда получим:
\[tg\alpha = \frac{g}{{{\omega ^2}{R_1}}}\]
Обратимся к рисунку – в прямоугольном треугольнике AOB видно, что тангенс угла \(\alpha\) равен:
\[tg\alpha = \frac{{R – h}}{{{R_1}}}\]
В итоге:
\[\frac{{R – h}}{{{R_1}}} = \frac{g}{{{\omega ^2}{R_1}}}\]
\[\omega = \sqrt {\frac{g}{{R – h}}} \]
Ответ: \(\omega = \sqrt {\frac{g}{{R – h}}}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.39 На конце стержня длиной 10 см укреплен груз массы 0,4 кг, приводимый во вращение
2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.42 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси с постоянной
