icodepro.ruУсловие задачи:
Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью \(\omega\) вокруг вертикальной оси. Вместе с чашей вращается шарик, лежащий на её внутренней поверхности. Расстояние от шарика до нижней точки чаши равно её радиусу. Определить угловую скорость вращения чаши.
Задача №2.4.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=0,8\) м, \(\omega-?\)
Решение задачи:
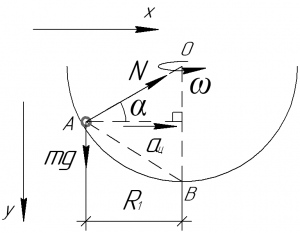Покажем на схеме силы, действующие на шарик (сила тяжести \(mg\) и сила реакции опоры \(N\)), и некоторые геометрические параметры задачи. Шарик не движется вдоль оси \(y\), поэтому запишем первый закон Ньютона в проекции на эту ось:
\[N \cdot \sin \alpha = mg\;\;\;\;(1)\]
Шарик движется по окружности в горизонтальной плоскости (вместе с чашей). Применим второй закон Ньютона в проекции на ось \(x\):
\[N \cdot \cos \alpha = m{a_ц}\]
Если шарик вращаются с угловой скоростью \(\omega\) на расстоянии \(R_1\) от оси вращения, то центростремительное ускорение \(a_ц\) можно найти по формуле:
\[{a_ц} = {\omega ^2}{R_1}\]
\[N \cdot \cos \alpha = m{\omega ^2}{R_1}\;\;\;\;(2)\]
Поделим равенства (2) и (1) друг на друга, тогда получим:
\[tg\alpha = \frac{g}{{{\omega ^2}{R_1}}}\;\;\;\;(3)\]
Нужно узнать угол \(\alpha\) и расстояние \(R_1\). Для этого рассмотрим треугольник AOB (смотрите схему). Он является равносторонним, так как две его стороны являются радиусами, а третья (AB) по условию равна \(R\). Отрезок \(R_1\) является высотой в равностороннем треугольнике, поэтому очевидно, что он равен:
\[{R_1} = \frac{{\sqrt 3 }}{2}R\]
Угол \(\alpha\) равен 30°, так как отрезок \(R_1\) также является биссектрисой в треугольник AOB. Значит:
\[tg\alpha = tg30^\circ = \frac{{\sqrt 3 }}{3}\]
В итоге равенство (3) примет вид:
\[\frac{{\sqrt 3 }}{3} = \frac{{2g}}{{{\omega ^2}\sqrt 3 R}}\]
\[\omega = \sqrt {\frac{{2g}}{R}} \]
Посчитаем ответ:
\[\omega = \sqrt {\frac{{2 \cdot 10}}{{0,8}}} = 5\; рад/с\]
Ответ: 5 рад/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.34 Тележка, скатившаяся по наклонному желобу с высоты 10 м, описывает в вертикальной
2.4.36 Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
Здравствуйте! Почему отсутствует сила трения? В аналогичных задачах, где тело вращается на горизонтальной платформе или на внутренней стенке цилиндра, она учитывается.
И еще у Вас нет осей на рисунке, хотя проекции векторов Вы записываете.
Во-первых, это шарик, а не какой-нибудь брусок, поэтому трением (обычно) можно пренебречь. На шарик, в отличие от бруска, действует сила трения качения (а не сила трения скольжения), которая обычно мала.
Во-вторых, шарик вращается вместе с чашей, значит их относительная скорость равна нулю, т.е. шарик не движется относительно чаши. В таком случае трения никакого нет.
Оси координат добавили, спасибо за замечание
Выражение N*cos(a)=m*aц должно относиться к проекции на ось Х, а не на ось У как ошибочно написано в тексте.
Исправил, спасибо!
Почему высота равна (?3xR)/2?
Общеизвестный факт, причем это легко показать. Дело в том, что равносторонний треугольник — это частный случай равнобедренного, когда его основание равно боковым сторонам. Известно, что высота h в равнобедренном (а значит и в равностороннем) треугольнике является ещё и медианой. Теперь запишите теорему Пифагора для прямоугольного треугольника, образованного высотой h, боковой стороной R и половиной основания R/2, то и получите высоту h, равную (?3xR)/2.